题目内容
（2013•莆田）已知在Rt△ABC中，∠C=90°，sinA=
，则tanB的值为
．
| 5 |
| 13 |
| 12 |
| 5 |
| 12 |
| 5 |
分析：根据题意作出直角△ABC，然后根据sinA=
，设一条直角边BC为5，斜边AB为13，根据勾股定理求出另一条直角边AC的长度，然后根据三角函数的定义可求出tnaB．
| 5 |
| 13 |
解答：解：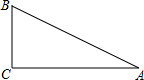
∵sinA=
，
∴设BC=5，AB=13，
则AC=
=12，
故tanB=
=
．
故答案为：
．
∵sinA=
| 5 |
| 13 |
∴设BC=5，AB=13，
则AC=
| AB2-BC2 |
故tanB=
| AC |
| BC |
| 12 |
| 5 |
故答案为：
| 12 |
| 5 |
点评：本题考查了互余两角三角函数的关系，属于基础题，解题的关键是掌握三角函数的定义和勾股定理的运用．
练习册系列答案
导学教程高中新课标系列答案
相关题目
