题目内容
【题目】如图所示,在△ABC中,AB=AC=5,D是BC上的点,DE∥AB交AC于点E,DF∥AC交AB于点F,那么四边形AFDE的周长是( ) 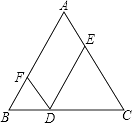
A.5
B.10
C.15
D.20
【答案】B
【解析】
由于DE∥AB,DF∥AC,则可以推出四边形AFDE是平行四边形,然后利用平行四边形的性质可以证明平行四边形AFDE的周长等于AB+AC.∵DE∥AB,DF∥AC,则四边形AFDE是平行四边形,∠B=∠EDC,∠FDB=∠C.∵AB=AC,∴∠B=∠C,∴∠B=∠FDB,∠C=∠EDF∴BF=FD,DE=EC,所以:平行四边形AFDE的周长等于AB+AC=10.故选B.
【考点精析】掌握等腰三角形的性质和平行四边形的判定是解答本题的根本,需要知道等腰三角形的两个底角相等(简称:等边对等角);两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.

练习册系列答案
相关题目