题目内容
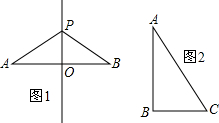
(1)如图1,已知?ABCD中,E为AD的中点,CE的延长线交BA的延长线于点F.求证:CD=FA.
(2)如图2,在小山东侧的A庄有一热气球,由于受西风的影响,以每分钟35米的速度沿着与水平方向成75°角的方向飞行,40分钟时到达C处.此时气球上的人发现气球与山顶P点及小山西侧的B庄在一条直线上,同时测得B庄的俯角为30°.又在A庄测得山顶P的仰角为45°.求A庄与B庄的距离及山高.(保留准确值)
解:(1)∵四边形ABCD是平行四边形,
∴CD∥AB.
又∵CE的延长线交BA的延长线于点F,
∴∠CDA=∠DAF.
∵E是AD中点,
∴DE=AE.
∵∠CED=∠AEF,
∴△CDE≌△AEF.
∴CD=AF.
(2)如图,过点A作AD⊥BC,垂足为D,
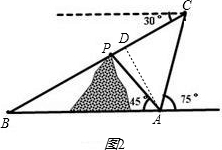
在Rt△ACD中,∠ACD=75°-30°=45°,
AC=35×40=1400(米),
∴AD=AC•sin45°=700 (米).
(米).
在Rt△ABD中,∠B=30°,
AB=2AD=1400 (米).
(米).
又过点P作PE⊥AB,垂足为E,
则AE=PE•tan45°=PE,
BE=PE•tan60°= PE,
PE,
∴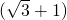 PE=1400
PE=1400  ,
,
∴PE=700(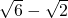 )(米).
)(米).
答:A庄与B庄的距离是1400 米,山高是700(
米,山高是700( 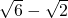 )米.
)米.
分析:(1)根据平行四边形的性质,-就可证明CD∥AB,∠CDA=∠DAF,又已知DE=AE,∠CED=∠AEF,符合全等三角形的判定中的ASA,即证△CDE≌△AEF,所以CD=AF.
(2)此题要先作AD⊥BC于D,PE⊥AB于E,则先求得AC的长,再求得AD的长、AB的长,然后在△PBA中,利用∠B和∠PAB的值求得PE的长.
点评:本题第一问考查了平行四边形的性质和全等三角形的判定的综合运用,也是基础题.本题第二问考查俯仰角的定义,要求学生能借助俯仰角构造直角三角形并解直角三角形.
∴CD∥AB.
又∵CE的延长线交BA的延长线于点F,
∴∠CDA=∠DAF.
∵E是AD中点,
∴DE=AE.
∵∠CED=∠AEF,
∴△CDE≌△AEF.
∴CD=AF.
(2)如图,过点A作AD⊥BC,垂足为D,

在Rt△ACD中,∠ACD=75°-30°=45°,
AC=35×40=1400(米),
∴AD=AC•sin45°=700
 (米).
(米).在Rt△ABD中,∠B=30°,
AB=2AD=1400
 (米).
(米).又过点P作PE⊥AB,垂足为E,
则AE=PE•tan45°=PE,
BE=PE•tan60°=
 PE,
PE,∴
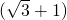 PE=1400
PE=1400  ,
,∴PE=700(
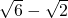 )(米).
)(米).答:A庄与B庄的距离是1400
 米,山高是700(
米,山高是700( 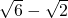 )米.
)米.分析:(1)根据平行四边形的性质,-就可证明CD∥AB,∠CDA=∠DAF,又已知DE=AE,∠CED=∠AEF,符合全等三角形的判定中的ASA,即证△CDE≌△AEF,所以CD=AF.
(2)此题要先作AD⊥BC于D,PE⊥AB于E,则先求得AC的长,再求得AD的长、AB的长,然后在△PBA中,利用∠B和∠PAB的值求得PE的长.
点评:本题第一问考查了平行四边形的性质和全等三角形的判定的综合运用,也是基础题.本题第二问考查俯仰角的定义,要求学生能借助俯仰角构造直角三角形并解直角三角形.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
 下列说法:
下列说法:


