题目内容
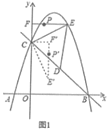
【题目】如图1,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD折叠,点C落在点C′的位置,BC′交AD于点G.
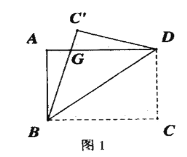
(1)求证:BG=DG;
(2)求C′G的长;
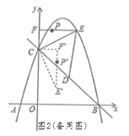
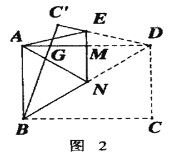
(3)如图2,再折叠一次,使点D与A重合,折痕EN交AD于M,求EM的长.
【答案】(1)见解析;(2)![]() cm;(3)
cm;(3)![]() .
.
【解析】
(1)由折叠性质知∠A=∠C′,AB=C′D,再利用“AAS”证△GAB≌△GC′D得BG=DG;
(2)设C′G=x,由全等性质知GD=BG=8-x,再在Rt△ABG中,利用勾股定理得x2+62=(8-x)2,解之可得答案;
(3)先求出BD=10,再证MN是△ABD的中位线得DN=![]() BD=5cm,MN=3cm,证EN=ED,设EM=x,则ED=EN=x+3,由勾股定理得ED2=EM2+DM2,即(x+3)2=x2+42,解之可得答案.
BD=5cm,MN=3cm,证EN=ED,设EM=x,则ED=EN=x+3,由勾股定理得ED2=EM2+DM2,即(x+3)2=x2+42,解之可得答案.
解:(1)证明:![]() 沿对角线
沿对角线![]() 对折,点
对折,点![]() 落在点
落在点![]() 的位置,
的位置,
![]() ,
,![]() ,
,
![]() 在
在![]() 与
与![]() 中,
中,
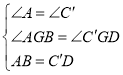 ,
,
![]() (AAS),
(AAS),
![]() ;
;
(2)![]()
![]()
设![]() ,则
,则![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() cm;
cm;
(3)![]() 点
点![]() 与点
与点![]() 重合,得折痕
重合,得折痕![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() 是
是![]() 的中位线,
的中位线,
![]() ,
,
在![]() 中,
中,
![]() ,
,
由折叠的性质可知![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
设![]() ,则
,则![]() ,
,
由勾股定理得![]() ,即
,即![]() ,
,
解得![]() ,即
,即![]() .
.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目