题目内容
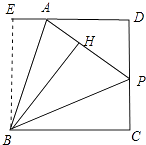
【题目】如图,已知四边形ABCD中,AD∥BC,∠C=90°,P是CD上一点,BH⊥AP于H,BH=BC=CD 
(1)求证:∠ABP=45°;
(2)若BC=20,PC=12,求AP的长.
【答案】
(1)证明:如图,作BE⊥DA于E,
∵AD∥BC,∠C=90°,
∴∠C+∠D=180°,
∴∠D=∠C=∠E=90°,
∴四边形BCDE是矩形,
∴BE=CD=BC=BH,
∵BH⊥AP,
∴∠AHB=∠BHP=90°,
在Rt△ABE和Rt△ABH中,
![]() ,
,
∴△ABE≌△ABH,
∴∠ABE=∠ABH,同理可证△PBH≌△PBC,
∴∠PBH=∠PBC,
∵∠EBC=90°,
∴2∠ABH+2∠PBH=90°,
∴∠ABH+∠PBH=45°,
∴∠ABP=45°
(2)证明:由(1)可知,四边形BCDE是矩形,
∵BC=CD,
∴四边形BCDE是正方形,
∴BC=CD=DE=BE=20,
∵△ABE≌△ABH,△PBH≌△PBC,
∴AE=AH,PC=PH,
∴AP=AE+PC,设AP=x,
则AE=x﹣12,AD=20﹣(x﹣12)=32﹣x,PD=8,
在Rt△ADP中,∵AD2+DP2=AP2,
∴(32﹣x)2+82=x2,
∴x=17,
∴AP=17.
【解析】(1)如图,作BE⊥DA于E,只要证明△ABE≌△ABH,△PBH≌△PBC,推出∠ABE=∠ABH,∠PBH=∠PBC,由∠EBC=90°,推出2∠ABH+2∠PBH=90°,由此即可证明.(2)首先证明AP=AE+PC,设PA=x,在Rt△ADP中,利用勾股定理列出方程即可解决问题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目