题目内容
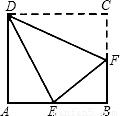
(2001•宁波)如图,四边形ABCD中,AB=AD,∠ABC=∠ADC,求证:AC⊥BD.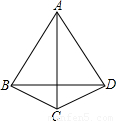
【答案】分析:先通过等边对等角得到∠CBD=∠CDB,即BC=CD,证明△ABC≌△ADC,得点B和D关于AC对称,所以AC⊥BD.
解答:证明:∵AB=AD,
∴∠ABD=∠ADB.
∵∠ABC=∠ADC,
∴∠CBD=∠CDB.
∴BC=CD.
则AB=AD,∠ABC=∠ADC,BC=CD,
∴△ABC≌△ADC.
∴∠BAC=∠DAC.
又AB=AD,
∴AC⊥BD.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.
解答:证明:∵AB=AD,
∴∠ABD=∠ADB.
∵∠ABC=∠ADC,
∴∠CBD=∠CDB.
∴BC=CD.
则AB=AD,∠ABC=∠ADC,BC=CD,
∴△ABC≌△ADC.
∴∠BAC=∠DAC.
又AB=AD,
∴AC⊥BD.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.

练习册系列答案
相关题目