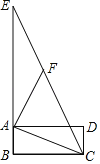Question

【题目】已知AB是半圆O的直径，M，N是半圆上不与A，B重合的两点，且点N在上.

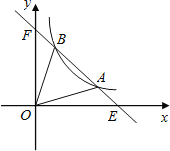
（1）如图1，MA＝6，MB＝8，∠NOB＝60°，求NB的长；

（2）如图2，过点M作MC⊥AB于点C，P是MN的中点，连接MB，NA，PC，试探究∠MCP，∠NAB，∠MBA之间的数量关系，并证明.

Answer 1

【答案】（1）5；（2）∠MCP＋∠MBA＋∠NAB＝90°，证明见解析

【解析】

（1）只要证明△OBN是等边三角形即可解决问题；

（2）结论：∠MCP+∠MBA+∠NAB=90°．如图2中，画⊙O，延长MC交⊙O于点Q，连接NQ，NB．关键是证明CP∥QN.

（1）如图1，∵AB是半圆O的直径，

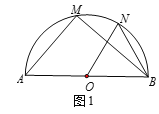
∴∠M＝90°．

在Rt△AMB中，AB＝

∴AB＝10.

∴OB＝5．

∵OB＝ON，

又∵∠NOB＝60°，

∴△NOB是等边三角形．

∴NB＝OB＝5．

（2）证明：如图2，

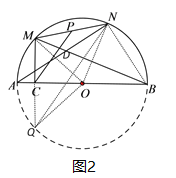
画⊙O，延长MC交⊙O于点Q，连接NQ，NB.

∵MC⊥AB，

又∵OM＝OQ，

∴MC＝CQ.

即C是MN的中点

又∵P是MQ的中点，

∴CP是△MQN的中位线.

∴CP∥QN.

∴∠MCP＝∠MQN.

∵∠MQN＝∠MON，∠MBN＝∠MON，

∴∠MQN＝∠MBN.

∴∠MCP＝∠MBN.

∵AB是直径，

∴∠ANB＝90°．

∴在△ANB中，∠NBA＋∠NAB＝90°.

∴∠MBN＋∠MBA＋∠NAB＝90°.

即∠MCP＋∠MBA＋∠NAB＝90°