题目内容
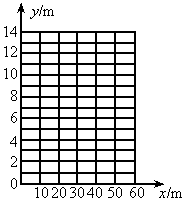
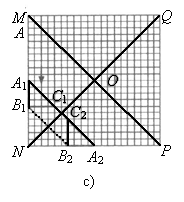
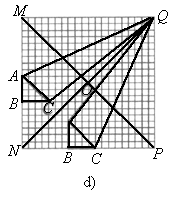
(2004·河北鹿泉)如图所示,在20×20的等距网格(每格的宽和高均是1个单位长)中,Rt△ABC从点A与点M重合的位置开始,以每秒1个单位长的速度先向下平移,当BC边与网格的底部重合时,继续以同样的速度向右平移,当点C与点P重合时,Rt△ABC停止移动,设运动时间为x秒,△QAC的面积为y.
(1)如图所示,当Rt△ABC向下平移到 的位置时,请你在网格图中画出
的位置时,请你在网格图中画出 关于直线QN成轴对称的图形;
关于直线QN成轴对称的图形;

(2)如图所示,在Rt△ABC向下平移的过程中,请你求出y与x的函数关系式,并说明当x分别取何值时,y取得最大值和最小值?最大值和最小值分别是多少?

(3)在Rt△ABC向右平移的过程中,请你说明当x分别取何值时,y取得最大值和最小值?最大值和最小值分别是多少?为什么?
答案:略
解析:
解析:
|
解 (1)如图所示, 是 是 关于直线QN成轴对称的图形, 关于直线QN成轴对称的图形,
(2)当△ABC以每秒1个单位长的速度向下平移x秒时(如图所示),则有: MA=x,MB=x+4,BC=4,MQ=20,
∴ 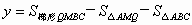
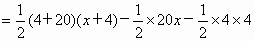
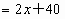 (0≤x≤16) (0≤x≤16)
由一次函数的性质可知: 当 x=0时,y取得最小值,且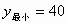 ; ;
当 x=16时,y取得最大值,且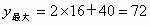
(3)解法1 当△ABC继续以每秒1个单位长的速度向右平移时,此时16≤x≤32, PB=20-(x-16)=36-x,PC=PB-4=32-x, ∴
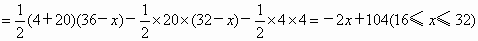
由一次函数的性质可知: 当 x=32时,y取得最小值,且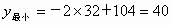 ; ;
当 x=16时,y最得最大值,且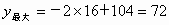 . .
解法 2 在△ABC自左向右平移的过程中,△QAC在每一时刻的位置都对应着如图所示中△QAC某一个时刻的位置,使得这样的两个三角形关于直线QN成轴对称.因此,根据轴对称的性质,只需考察△ABC在自上至下平移过程中△QAC面积的变化情况,便可以知道△ABC在自左向右平移过程中△QAC面积的变化情况.∴当 x=16时,y取得最大值,且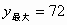 ; ;
当 x=32时,y取得最小值,且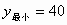 . . |

练习册系列答案
相关题目
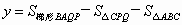
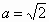 ,b=1时,求
,b=1时,求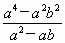 的值.
的值.