题目内容
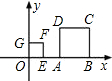 如图,正方形OEFG和正方形ABCD是位似形,点F的坐标为(1,1),点C的坐标为(4,2),则这两个正方形位似中心的坐标是
如图,正方形OEFG和正方形ABCD是位似形,点F的坐标为(1,1),点C的坐标为(4,2),则这两个正方形位似中心的坐标是分析:两个位似图形的主要特征是:每对位似对应点与位似中心共线;不经过位似中心的对应线段平行.则位似中心就是两对对应点的延长线的交点.
解答: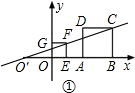 解:①两个图形位似时,位似中心就是CF与x轴的交点,
解:①两个图形位似时,位似中心就是CF与x轴的交点,
设直线CF解析式为y=kx+b,将C(4,2),F(1,1)代入,得
,解得
,即y=
x+
,
令y=0得x=-2,
∴O′坐标是(-2,0);
②当位似中心O′在两个正方形之间时,
直线OC的解析式为:y=2x,
直线BG的解析式为:y=-
x+1,
联立:
,
解得:
,
∴O′坐标是(
,
).
故本题答案为:(-2,0)或(
,
).
 解:①两个图形位似时,位似中心就是CF与x轴的交点,
解:①两个图形位似时,位似中心就是CF与x轴的交点,设直线CF解析式为y=kx+b,将C(4,2),F(1,1)代入,得
|
|
| 1 |
| 3 |
| 2 |
| 3 |
令y=0得x=-2,
∴O′坐标是(-2,0);
②当位似中心O′在两个正方形之间时,
直线OC的解析式为:y=2x,
直线BG的解析式为:y=-
| 1 |
| 4 |
联立:
|
解得:
|
∴O′坐标是(
| 4 |
| 3 |
| 2 |
| 3 |
故本题答案为:(-2,0)或(
| 4 |
| 3 |
| 2 |
| 3 |
点评:本题主要考查位似图形的性质,每对位似对应点与位似中心共线.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
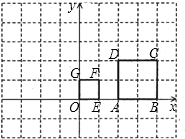 如图,正方形OEFG和正方形ABCD是位似图形,且点F与点C是一对对应点,点F的坐标是(1,1),点C的坐标是(4,2);则它们的位似中心的坐标是( )
如图,正方形OEFG和正方形ABCD是位似图形,且点F与点C是一对对应点,点F的坐标是(1,1),点C的坐标是(4,2);则它们的位似中心的坐标是( )| A、(0,0) | B、(-1,0) | C、(-2,0) | D、(-3,0) |
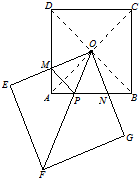 29、如图,正方形OEFG绕着正方形ABCD的对角线的交点O旋转,边OE、OG分别交边AD、AB于点M、N.
29、如图,正方形OEFG绕着正方形ABCD的对角线的交点O旋转,边OE、OG分别交边AD、AB于点M、N.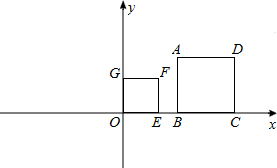 (2010•安庆二模)如图,正方形OEFG和正方形ABCD的是位似图形,若点A的坐标为(2,2),位似中心的坐标是(-4,0),则点F的坐标为
(2010•安庆二模)如图,正方形OEFG和正方形ABCD的是位似图形,若点A的坐标为(2,2),位似中心的坐标是(-4,0),则点F的坐标为 如图,正方形OEFG绕着正方形ABCD的对角线的交点O旋转,边OE、OG分别交边AD、AB于点M、N.
如图,正方形OEFG绕着正方形ABCD的对角线的交点O旋转,边OE、OG分别交边AD、AB于点M、N.