Question

如图，在△ABC中，AB=AC=5，BC=6，点P、Q分别在AB、AC上，其中点P从A开始，向点B以1个单位/s的速度行进，点Q从点C开始，以1个单位/s 的速度向A行进，P、Q两点同时出发，运行的时间为x秒，作PE⊥BC于点E，QF⊥BC于点F．
（1）当点P运行到AB中点的时候，求四边形PEFQ的面积．
（2）在P、Q运行过程中，四边形PEFQ的面积S是否发生变化？如果发生变化，写出S与x之间的函数关系式，如果不发生变化，求出S的值；
（3）设线段PQ的中点为G，在P、Q的运行过程中，G的运行路线是什么？说明理由．

Answer 1

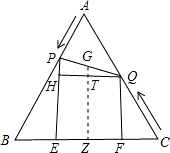解：（1）作AK⊥BC于K，
∵△ABC是等腰三角形，BC=6，
∴BK=CK=3，
∵AB=5，根据勾股定理得：AK=4，
∴sinB=sinC=，cosB=cosC=，
当P运行到AB中点时，由题意可得AP=AQ=，
PQ为△ABC的中位线，PQ=3，
∴四边形PEFQ是矩形，PE=PB•sinB==2，
∴四边形PEFQ的面积=2×3=6，
答：当点P运行到AB中点的时候，四边形PEFQ的面积是6．

（2）解：不变，
∵AP=CQ=x，
∴BP=AQ=5-x，
在Rt△BPE中，BE=BP•cosB=（5-x），
在Rt△CQF中，CF=CQ•cosC=x，
∴BE+CF=（5-x）+x=3，
∴EF=6-3=3
同理可得：PE+QF=×5=4，
∴S=（PE+QF）×EF=×4×3=6．
答：不变，S的值是6．

（3）解：点Q的运行路线是△ABC中平行于BC的中位线，
当x=0时，G在AC的中点（设为M）处，
当x=5时，G在AB的中点（设为N）处，
由（1）可得ME=NF=2，
当0＜x＜5时，如图，作GZ⊥BC于Z，QH⊥PE于H，交GZ于T，
易证GT是△PHQ的中位线，GT=PH，四边形TZEH是矩形，TZ=（HE+QF），
∴GZ=（PE+QF）=2
∴点Q在MN上，
∴点Q的运行路线是点Q的运行路线是△ABC中平行于BC的中位线，
答：线段PQ的中点为G，在P、Q的运行过程中，G的运行路线是△ABC中平行于BC的中位线．
分析：（1）作AK⊥BC于K，根据等腰三角形的性质求出BK=CK=3，根据勾股定理求出AG，进一步求出sinB=sinC=，cosB=cosC=，由PQ为△ABC的中位线求出PQ，PE，根据面积公式求出即可；
（2）求出BE=BP•cosB=（5-x），CF=CQ•cosC=x，得出BE+CF=3，求出EF长，同理可得：PE+QF=×5=4，即可求出面积；
（3）点Q的运行路线是△ABC中平行于BC的中位线，分为以下几种情况：当x=0时，G在AC的中点（设为M）处；当x=5时，G在AB的中点（设为N）处；当0＜x＜5时，如图，作GZ⊥BC于Z，QH⊥PE于H，交GZ于T，由（1）可证Q在中位线上；即可得到答案．
点评：本题主要考查对等腰三角形的性质，直角三角形的性质，矩形的性质和判定，勾股定理，锐角三角函数的定义等知识点的理解和掌握，能综合运用性质进行计算是解此题的关键，题型较好，难度适中．