题目内容
 如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,折痕DE分别交AB、AC于点E、G,连接GF.下列结论:
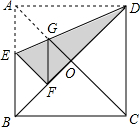
如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,折痕DE分别交AB、AC于点E、G,连接GF.下列结论:①∠AGD=112.5°;②tan∠AED=2;③△AGD的面积=△OGD的面积;④AE=GF;⑤BE=2OG.
其中正确结论的序号是( )
分析:①由四边形ABCD是正方形,可得∠GAD=∠ADO=45°,又由折叠的性质,可求得∠ADG的度数,然后利用三角形外角的性质,求得∠AGD=112.5°;
②由AE=EF<BE,可得AD>2AE,即可得tan∠AED
>2;
③由AG=GF>OG,可得△AGD的面积>△OGD的面积;
④由折叠的性质与平行线的性质,易得△EFG是等腰三角形,即可证得AE=GF;
⑤易证得四边形AEFG是菱形,由等腰直角三角形的性质,即可得BE=2OG.
②由AE=EF<BE,可得AD>2AE,即可得tan∠AED
| AD |
| AE |
③由AG=GF>OG,可得△AGD的面积>△OGD的面积;
④由折叠的性质与平行线的性质,易得△EFG是等腰三角形,即可证得AE=GF;
⑤易证得四边形AEFG是菱形,由等腰直角三角形的性质,即可得BE=2OG.
解答:解:∵四边形ABCD是正方形,
∴∠GAD=∠ADO=45°,
由折叠的性质可得:∠ADG=
∠ADO=22.5°,
∴∠AGD=180°-∠GAD-∠ADG=112.5°,
故①正确.
∵tan∠AED=
,
由折叠的性质可得:AE=EF,∠EFD=∠EAD=90°,
∴AE=EF<BE,
∴AE<
AB,
∴tan∠AED=
>2,
故②错误.
∵∠AOB=90°,
∴AG=FG>OG,△AGD与△OGD同高,
∴S△AGD>S△OGD,
故③错误.
∵∠EFD=∠AOF=90°,
∴EF∥AC,
∴∠FEG=∠AGE,
∵∠AGE=∠FGE,
∴∠FEG=∠FGE,
∴EF=GF,
∵AE=EF,
∴AE=GF,
故④正确.
∵AE=EF=GF,AG=GF,
∴AE=EF=GF=AG,
∴四边形AEFG是菱形,
∴∠OGF=∠OAB=45°,
∴EF=GF=
OG,
∴BE=
EF=
×
OG=2OG.
故⑤正确.
∴其中正确结论的序号是:①④⑤.
∴∠GAD=∠ADO=45°,
由折叠的性质可得:∠ADG=
| 1 |
| 2 |
∴∠AGD=180°-∠GAD-∠ADG=112.5°,
故①正确.
∵tan∠AED=
| AD |
| AE |
由折叠的性质可得:AE=EF,∠EFD=∠EAD=90°,
∴AE=EF<BE,
∴AE<
| 1 |
| 2 |
∴tan∠AED=
| AD |
| AE |
故②错误.
∵∠AOB=90°,
∴AG=FG>OG,△AGD与△OGD同高,
∴S△AGD>S△OGD,
故③错误.
∵∠EFD=∠AOF=90°,
∴EF∥AC,
∴∠FEG=∠AGE,
∵∠AGE=∠FGE,
∴∠FEG=∠FGE,
∴EF=GF,
∵AE=EF,
∴AE=GF,
故④正确.
∵AE=EF=GF,AG=GF,
∴AE=EF=GF=AG,
∴四边形AEFG是菱形,
∴∠OGF=∠OAB=45°,
∴EF=GF=
| 2 |
∴BE=
| 2 |
| 2 |
| 2 |
故⑤正确.
∴其中正确结论的序号是:①④⑤.
点评:此题考查了正方形的性质、折叠的性质、等腰直角三角形的性质以及菱形的判定与性质等知识.此题综合性较强,难度较大,注意掌握折叠前后图形的对应关系,注意数形结合思想的应用.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
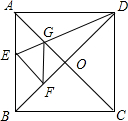 如图,在正方形纸片ABCD中,对角线AC,BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合.展开后,折痕DE分别交AB,AC于点E,G.连接GF.下列结论:①∠AGD=112.5°;②tan∠AED=2;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG.其中正确结论的个数是( )
如图,在正方形纸片ABCD中,对角线AC,BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合.展开后,折痕DE分别交AB,AC于点E,G.连接GF.下列结论:①∠AGD=112.5°;②tan∠AED=2;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG.其中正确结论的个数是( )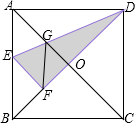 如图,在正方形纸片ABCD中,对角线AC,BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合.展开后,折痕DE分别交AB,AC于点G,E,连接GF.
如图,在正方形纸片ABCD中,对角线AC,BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合.展开后,折痕DE分别交AB,AC于点G,E,连接GF.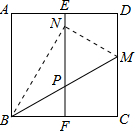 如图,在正方形纸片ABCD中,E,F分别是AD,BC的中点,沿过点B的直线折叠,使点C落在EF上,落点为N,折痕交CD边于点M,BM与EF交于点P,再展开.则下列结论中:①CM=DM;②∠ABN=30°;③AB2=3CM2;④△PMN是等边三角形.正确的有( )
如图,在正方形纸片ABCD中,E,F分别是AD,BC的中点,沿过点B的直线折叠,使点C落在EF上,落点为N,折痕交CD边于点M,BM与EF交于点P,再展开.则下列结论中:①CM=DM;②∠ABN=30°;③AB2=3CM2;④△PMN是等边三角形.正确的有( )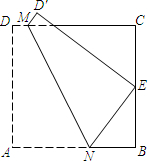 (2013•大庆模拟)如图,在正方形纸片ABCD中,E为BC的中点.将纸片折叠,使点A与点E重合,点D落在点D′处,MN为折痕.若梯形ADMN的面积为S1,梯形BCMN的面积为S2,则
(2013•大庆模拟)如图,在正方形纸片ABCD中,E为BC的中点.将纸片折叠,使点A与点E重合,点D落在点D′处,MN为折痕.若梯形ADMN的面积为S1,梯形BCMN的面积为S2,则