题目内容
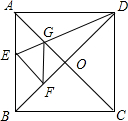 如图,在正方形纸片ABCD中,对角线AC,BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合.展开后,折痕DE分别交AB,AC于点E,G.连接GF.下列结论:①∠AGD=112.5°;②tan∠AED=2;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG.其中正确结论的个数是( )
如图,在正方形纸片ABCD中,对角线AC,BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合.展开后,折痕DE分别交AB,AC于点E,G.连接GF.下列结论:①∠AGD=112.5°;②tan∠AED=2;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG.其中正确结论的个数是( )| A、1 | B、2 | C、3 | D、4 |
分析:解决此类问题,应结合题意,最好实际操作图形的折叠,易于找到图形间的关系.
解答:解:因为∠GAD=45°,由折叠可知:∠ADG=∠ODG=22.5°.故:
①∠AGD=180°-45°-22.5°=112.5°正确;
②设OG=1,则AG=GF=
,
又∠BAG=45°,∠AGE=67.5°,∴∠AEG=67.5°,
∴AE=AG=
,则AC=2AO=2(
+1),
∴AD=
=2+
,
tan∠AED=
=
+1,错误;
③由折叠可知:AG=FG,在直角三角形GOF中,
斜边GF>直角边OG,故AG>OG,两三角形的高相同,
则S△AGD>S△OGD,故错误;
④中,AE=EF=FG=AG,故正确;
⑤∵GF=EF,
∴BE=
EF=
GF=
•
OG=2OG,
∴BE=2OG
故正确.
故选C.
①∠AGD=180°-45°-22.5°=112.5°正确;
②设OG=1,则AG=GF=
| 2 |
又∠BAG=45°,∠AGE=67.5°,∴∠AEG=67.5°,
∴AE=AG=
| 2 |
| 2 |
∴AD=
2(
| ||
|
| 2 |
tan∠AED=
| AD |
| AE |
| 2 |
③由折叠可知:AG=FG,在直角三角形GOF中,
斜边GF>直角边OG,故AG>OG,两三角形的高相同,
则S△AGD>S△OGD,故错误;
④中,AE=EF=FG=AG,故正确;
⑤∵GF=EF,
∴BE=
| 2 |
| 2 |
| 2 |
| 2 |
∴BE=2OG
故正确.
故选C.
点评:本题通过折叠变换考查学生的逻辑思维能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
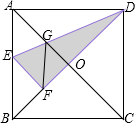 如图,在正方形纸片ABCD中,对角线AC,BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合.展开后,折痕DE分别交AB,AC于点G,E,连接GF.
如图,在正方形纸片ABCD中,对角线AC,BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合.展开后,折痕DE分别交AB,AC于点G,E,连接GF.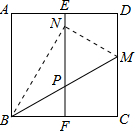 如图,在正方形纸片ABCD中,E,F分别是AD,BC的中点,沿过点B的直线折叠,使点C落在EF上,落点为N,折痕交CD边于点M,BM与EF交于点P,再展开.则下列结论中:①CM=DM;②∠ABN=30°;③AB2=3CM2;④△PMN是等边三角形.正确的有( )
如图,在正方形纸片ABCD中,E,F分别是AD,BC的中点,沿过点B的直线折叠,使点C落在EF上,落点为N,折痕交CD边于点M,BM与EF交于点P,再展开.则下列结论中:①CM=DM;②∠ABN=30°;③AB2=3CM2;④△PMN是等边三角形.正确的有( )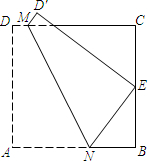 (2013•大庆模拟)如图,在正方形纸片ABCD中,E为BC的中点.将纸片折叠,使点A与点E重合,点D落在点D′处,MN为折痕.若梯形ADMN的面积为S1,梯形BCMN的面积为S2,则
(2013•大庆模拟)如图,在正方形纸片ABCD中,E为BC的中点.将纸片折叠,使点A与点E重合,点D落在点D′处,MN为折痕.若梯形ADMN的面积为S1,梯形BCMN的面积为S2,则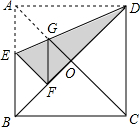 如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,折痕DE分别交AB、AC于点E、G,连接GF.下列结论:
如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,折痕DE分别交AB、AC于点E、G,连接GF.下列结论: