题目内容
【题目】如图，在平面直角坐标系xOy中，直线AB经过点A（6，0）、B（0，6），⊙O的半径为2（O为坐标原点），点P是直线AB上的一动点，过点P作⊙O的一条切线PQ，Q为切点，则切线长PQ的最小值为（ ）
A.
B.3
C.3 
D.
【答案】D
【解析】连接OP、OQ．
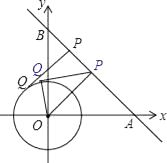
∵PQ是⊙O的切线，
∴OQ⊥PQ；
根据勾股定理知PQ2=OP2﹣OQ2，
∵当PO⊥AB时，线段PQ最短；
又∵A（﹣6，0）、B（0，6），
∴OA=OB=6，
∴AB=6 
∠BOP=45°，即OP是Rt△AOB斜边上的中线，
∴OP= 
AB=3 ，
∵OQ=2，
∴PQ= 
，
所以答案是：D．
【考点精析】本题主要考查了垂线段最短和直角三角形斜边上的中线的相关知识点，需要掌握连接直线外一点与直线上各点的所有线段中，垂线段最短；现实生活中开沟引水，牵牛喝水都是“垂线段最短”性质的应用；直角三角形斜边上的中线等于斜边的一半才能正确解答此题．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
