题目内容
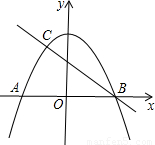
如图,抛物线y1=-ax2-ax+1经过点P![]() ,且与抛物线y2=ax2-ax-1,相交于A,B两点.
,且与抛物线y2=ax2-ax-1,相交于A,B两点.

(1)求a值;
(2)设y1=-ax2-ax+1与x轴分别交于M,N两点(点M在点N的左边),y2=ax2-ax-1与x轴分别交于E,F两点(点E在点F的左边),观察M,N,E,F四点的坐标,写出一条正确的结论,并通过计算说明;
(3)设A,B两点的横坐标分别记为xA,xB,若在x轴上有一动点Q(x,0),且xA≤≤x≤xB,过Q作一条垂直于x轴的直线,与两条抛物线分别交于C,D两点,试问当x为何值时,线段CD有最大值?其最大值为多少?
答案:
解析:

解析:
解(1)∵点P(![]() )在抛物线
)在抛物线![]() 上,
上,
∴![]() . 2分
. 2分
解得![]() . 3分
. 3分
(2)由(1)知![]() ,∴抛物线
,∴抛物线![]() . 5分
. 5分
当![]() 时,解得
时,解得![]()
∵点M在点N的左边,∴![]() 6分
6分
当![]() 时,解得
时,解得![]() .
.
∵点E在点F的左边,∴![]() . 7分
. 7分
∵![]() ,
,![]() .
.
∴点M与点F对称,点N与点E对称. 8分

(3)∵![]()
∴抛物线y1开口向下,抛物线y2开口向上. 9分
根据题意,得CD=y1-y2=![]() 11分
11分
∵![]() ∴当x=0时,CD有最大值2. 12分
∴当x=0时,CD有最大值2. 12分
说明:第(2)问中,结论写成“M、N、E、F四点横坐标的代数式和为0”或“MN=EF”均得1分.


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
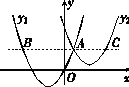

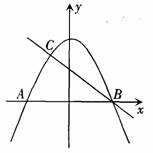
 x2+3与x轴交于A、B两点,与直线y2=-
x2+3与x轴交于A、B两点,与直线y2=-