题目内容
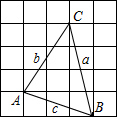如图，在方格纸（每个小方格都是边长为1个单位长度的正方形）中，我们称每个小正方形的顶点为格点，以格点为顶点的图形称为格点图形，图中的△ABC为格点三角形，它的三边a，b，c的大小关系是（ ）| A、b＜c＜a | B、a＜c＜b | C、c＜b＜a | D、b＜a＜c |
分析：由已知每个小方格都是边长为1个单位长度的正方形，所以先根据勾股定理分别求出a、b、c，在进行比较得出选项．
解答：解：根据已知格点三角形，由勾股定理得：
a2=12+42=17，∴a=
，
b2=22+32=13，∴b=
，
c2=12+32=10，∴c=
，
＜
＜
，
∴c＜b＜a．
故选C．
a2=12+42=17，∴a=
| 17 |
b2=22+32=13，∴b=
| 13 |
c2=12+32=10，∴c=
| 10 |
| 10 |
| 13 |
| 17 |
∴c＜b＜a．
故选C．
点评：此题考查的是勾股定理及实数大小的比较，解题的关键是先由已知根据勾股定理求出a、b、c，再进行比较．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
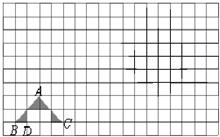22、如图，在方格纸（每个小方格都是边长为1个单位长度的正方形）中，我们称每个小正方形的顶点为格点，以格点为顶点的图形称为格点图形．如图中的△ABC称为格点△ABC．
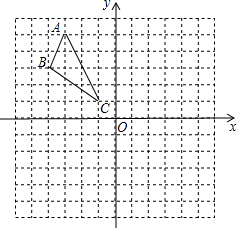如图，在方格纸中每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点A的坐标为（-3，5）．
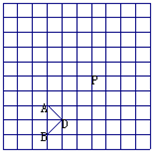如图，在方格纸（每个小方格都是边长为1个单位长度的正方形）中，我们称每个小正方形的顶点为格点，以格点为顶点的图形称为格点图形．如图中的△ABD称为格点△ABD．
如图，在方格纸（每个小方格都是边长为1个单位长度的正方形）上，并且图形的顶点均在格点上，请结合所给的方格纸解答下列问题：