题目内容
【题目】综合与探究
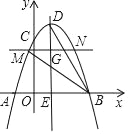
如图,抛物线y=﹣![]() x2+2x+6与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,其对称轴与抛物线交于点D.与x轴交于点E.
x2+2x+6与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,其对称轴与抛物线交于点D.与x轴交于点E.
(1)求点A,B,D的坐标;
(2)点G为抛物线对称轴上的一个动点,从点D出发,沿直线DE以每秒2个单位长度的速度运动,过点C作x轴的平行线交抛物线于M,N两点(点M在点N的左边).
设点G的运动时间为ts.
①当t为何值时,以点M,N,B,E为顶点的四边形是平行四边形;
②连接BM,在点G运动的过程中,是否存在点M.使得∠MBD=∠EDB,若存在,求出点M的坐标;若不存在,请说明理由;
(3)点Q为坐标平面内一点,以线段MN为对角线作萎形MENQ,当菱形MENQ为正方形时,请直接写出t的值.
【答案】(1)A(﹣2,0),B(6,0);D(2,8);(2)①见解析;②存在,理由见解析;
(3)t=![]() .
.
【解析】分析:(1)令y=0,解方程﹣![]() x2+2x+6=0,即可求出A、B点的坐标,把y=﹣
x2+2x+6=0,即可求出A、B点的坐标,把y=﹣![]() x2+2x+6改写成顶点式,根据二次函数的性质求出D点的坐标;
x2+2x+6改写成顶点式,根据二次函数的性质求出D点的坐标;
(2)①要使四边形MEBN为平行四边形,则MN=BE=4,根据二次函数的对称性求出点M的坐标,从而求出DG的长,由DG=2t可求出t的值;②设BM交DE于P,如图,设P(2,m),在Rt△BEP中,根据PE2+BE2=PB2,列方程求出m的值,用待定系数法求出直线BP的解析式,与二次函数解析式联立,可求出点M的坐标;
(3)由正方形的性质得GN=GE=8﹣2t,从而表示出点N的坐标,把点N的坐标代入二次函数解析式求出t的值.
详解:(1)当y=0时,﹣![]() x2+2x+6=0,解得x1=﹣2,x2=6,则A(﹣2,0),B(6,0);
x2+2x+6=0,解得x1=﹣2,x2=6,则A(﹣2,0),B(6,0);
∵y=﹣![]() (x﹣2)2+8,
(x﹣2)2+8,
∴D(2,8);
(2)①∵E(2,0),B(6,0),
∴BE=4,
∵四边形MEBN为平行四边形,
∴MN=BE=4,
∵MN∥x轴,
∴MG=NG=2,
∴M点的横坐标为0,此时M(0,6)
∴2t=8﹣6,解得t=1,
∴当t为1s时,以点M,N,B,E为顶点的四边形是平行四边形;
②存在.
设BM交DE于P,如图,设P(2,m)
∵∠MBD=∠EDB,
∴PD=PB=8﹣m,
在Rt△BEP中,∵PE2+BE2=PB2,
∴m2+42=(8﹣m)2,解得m=5,
∴P(2,3),
设直线BP的解析式为y=px+q,
把B(6,0),P(2,3)代入得![]() ,解得
,解得![]() ,
,
∴直线BP的解析式为y=﹣![]() x+
x+![]() ,
,
解方程组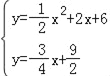 得
得![]() 或
或![]() ,
,
∴M点的坐标为(﹣![]() ,
,![]() );
);
(3)GE=8﹣2t,
∵菱形MENQ为正方形时,
∴GN=GE=8﹣2t,
∴N(10﹣2t,8﹣2t),
把N(10﹣2t,8﹣2t)代入y=﹣![]() x2+2x+6得﹣
x2+2x+6得﹣![]() (10﹣2t)2+2(10﹣2t)+6=8﹣2t,
(10﹣2t)2+2(10﹣2t)+6=8﹣2t,
整理得t2﹣9t+16,
∴t=![]() .
.

 阅读快车系列答案
阅读快车系列答案