题目内容
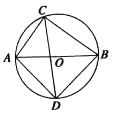
【题目】如图,![]() 的直径
的直径![]() 为
为![]() ,弦
,弦![]() 为
为![]() ,
,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,求
,求![]() ,
,![]() ,
,![]() 的长.
的长.
【答案】BC=8,AD=BD=5![]() .
.
【解析】
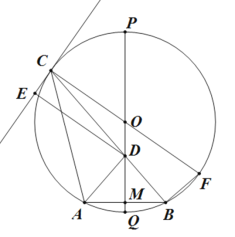
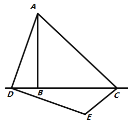
根据直径所对的圆周角等于90°可得∠ACB=90°,利用勾股定理可求出BC的长,利用角平分线的定义及圆周角定理可得∠ABD=∠ACD=45°,∠DAB=∠DCB=45°,可得△ABD是等腰直角三角形,即可求出AD、BD的长.
∵AB为直径,∠ACB是AB所对的圆周角,
∴∠ACB=90°,
∵AB=10,AC=6,
∴BC=![]() =
=![]() =8,
=8,
∵CD是∠ACB的角平分线,
∴∠ACD=∠DCB=![]() ∠ACB=45°,
∠ACB=45°,
∵∠ACD和∠ABD是![]() 所对的圆周角,
所对的圆周角,
∴∠ACD=∠ABD=45°,
同理可得:∠DAB=∠DCB=45°,
∴∠DAB=∠DBA=45°,
∴△ABD是等腰直角三角形,
∴2AD2=AB2,
∴AD=BD=5![]() .
.

练习册系列答案
相关题目
【题目】为了解我市居民用水情况,在某小区随机抽查了20户家庭,并将这些家庭的月用水量进行统计,结果如下表:
月用水量(吨) | 4 | 5 | 6 | 8 | 13 |
户数 | 4 | 5 | 7 | 3 | 1 |
则关于这20户家庭的月用水量,下列说法正确的是( )
A.中位数是5B.平均数是5C.众数是6D.方差是6