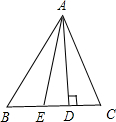
题目内容
说理解答题
在空白处填上适当的内容(理由或数学式)
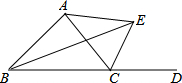
解:在ABC中
∠B+∠ACB+∠BAC=180°______
∴∠BAC=180°-∠B-______(等式的性质)
=180°-36°-110°=______
∵AE是∠BAC的平分线(已知)
∴∠CAE=______∠BAC=17°
∵AD是BC边上的高即AD⊥BC(已知)
∴∠D=______
∵∠ACE是△ACD的外角(已知)
∴∠ACE=∠CAD+∠D______
∴∠CAD=∠ACE-∠D(等式的性质)
=110°-90°═20°
∴∠DAE=∠CAD+______
=20°+17°
=______.
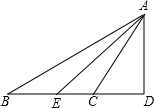
在空白处填上适当的内容(理由或数学式)
解:在ABC中
∠B+∠ACB+∠BAC=180°______
∴∠BAC=180°-∠B-______(等式的性质)
=180°-36°-110°=______
∵AE是∠BAC的平分线(已知)
∴∠CAE=______∠BAC=17°
∵AD是BC边上的高即AD⊥BC(已知)
∴∠D=______
∵∠ACE是△ACD的外角(已知)
∴∠ACE=∠CAD+∠D______
∴∠CAD=∠ACE-∠D(等式的性质)
=110°-90°═20°
∴∠DAE=∠CAD+______
=20°+17°
=______.

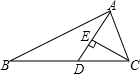
在ABC中,
∵∠B+∠ACB+∠BAC=180°(三角形内角和定理)
∴∠BAC=180°-∠B-∠BCA(等式的性质)
=180°-36°-110°=34°
∵AE是∠BAC的平分线(已知)
∴∠CAE=
∠BAC=17°
∵AD是BC边上的高即AD⊥BC(已知)
∴∠D=90°,
∵∠ACE是△ACD的外角(已知)
∴∠ACE=∠CAD+∠D(三角形外角的性质)
∴∠CAD=∠ACE-∠D(等式的性质)
=110°-90°=20°
∴∠DAE=∠CAD+∠CAE
=20°+17°
=37°.
故答案为:三角形内角和定理;∠BAC;34°;
;90°;三角形外角的性质;∠CAE;37°.
∵∠B+∠ACB+∠BAC=180°(三角形内角和定理)
∴∠BAC=180°-∠B-∠BCA(等式的性质)
=180°-36°-110°=34°
∵AE是∠BAC的平分线(已知)
∴∠CAE=
| 1 |
| 2 |
∵AD是BC边上的高即AD⊥BC(已知)
∴∠D=90°,
∵∠ACE是△ACD的外角(已知)
∴∠ACE=∠CAD+∠D(三角形外角的性质)
∴∠CAD=∠ACE-∠D(等式的性质)
=110°-90°=20°
∴∠DAE=∠CAD+∠CAE
=20°+17°
=37°.
故答案为:三角形内角和定理;∠BAC;34°;
| 1 |
| 2 |

练习册系列答案
相关题目