��Ŀ����
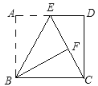
����Ŀ����ͼ1������ֱ������ֽ�壨Rt��ABC��Rt��BDE������ͼ��ʾ�ķ�ʽ�ڷţ��غϵ�ΪB�������С�BDE����ACB��90�㣬��ABC��30�㣬BD��DE��AC��2������BDE���ŵ�B˳ʱ����ת��
��1������D��BC��ʱ����CD�ij���
��2������BDE��ת��A��D��E���㹲��ʱ��������Ӧ�IJ�ͼ�����CDE�����
��3����ͼ2������CD����G��CD���е㣬����AG����AG�����ֵ����Сֵ��
���𰸡���1��2![]() ��2����2��1����3��AG����СֵΪ
��2����2��1����3��AG����СֵΪ![]() ��1��AG�����ֵΪ
��1��AG�����ֵΪ![]() +1
+1
��������
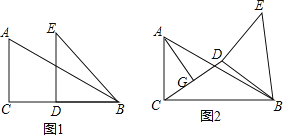
��1����ͼ1�У�����CD��BC��BD��ֻҪ���BC���ɽ�����⣻
��2�����������ηֱ���⣬�������ε������ʽ�ɽ�����⣻
��3����ͼ4�У�ȡBC���е�H������GH����CG��GD��CH��HB���Ƴ�HG��![]() BD��1���ɵõ�G���˶��켣����HΪԲ��1Ϊ�뾶��Բ�����ݵ���Բ��λ�ù�ϵ���ɽ�����⣻
BD��1���ɵõ�G���˶��켣����HΪԲ��1Ϊ�뾶��Բ�����ݵ���Բ��λ�ù�ϵ���ɽ�����⣻
�⣺��1����ͼ1�У�

��Rt��ABC�У��ߡ�C��90�㣬AC��2����ABC��30�㣬
��BC��AC��tan30�㣽2![]() ��
��
��BD��2��
��CD��BC��BD��2![]() ��2��
��2��
��2����ͼ2�У���A��D��E����ʱ����֤�ı���ACBD�Ǿ��Σ�

��S��CDE��![]() ��DE��CA��
��DE��CA��![]() ��2��2��2��
��2��2��2��
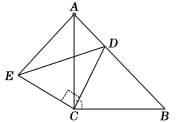
��ͼ3�У���A��E��D����ʱ����CH��AD��H��
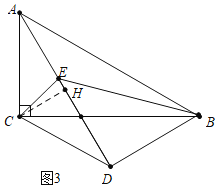
��Rt��ADB����AB��2BD��
���BAD��30�㣬
�ߡ�CAB��60�㣬
���CAH��30�㣬
��CH��![]() AC��1��
AC��1��
��S��CDE��![]() ��DE��CH��
��DE��CH��![]() ��2��1��1��
��2��1��1��
��3����ͼ4�У�ȡBC���е�H������GH��
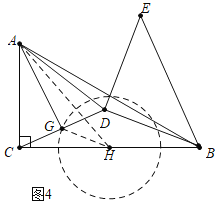
��CG��GD��CH��HB��
��HG��![]() BD��1��
BD��1��
���G���˶��켣����HΪԲ��1Ϊ�뾶��Բ��
��Rt��ACH��AH��![]() ��
��![]() ��
��![]() ��
��
��AG����Сֵ��AH��GH��![]() ��1��
��1��
AG�����ֵ��AH+GH��![]() +1
+1

 ���ѵ����Ԫ��ĩ���100��ϵ�д�
���ѵ����Ԫ��ĩ���100��ϵ�д� ��˼άС�ھ�100����ҵ��ϵ�д�
��˼άС�ھ�100����ҵ��ϵ�д� ��ʦָ��һ��ͨϵ�д�
��ʦָ��һ��ͨϵ�д�