题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 在
在![]() 内并排
内并排![]() 不重叠
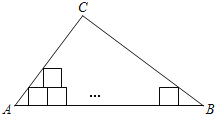
不重叠![]() 放入边长为1的小正方形纸片,第一层小纸片的一条边都在AB上,首尾两个正方形各有一个顶点分别在AC、BC上,依次这样摆放上去,则最多能摆放
放入边长为1的小正方形纸片,第一层小纸片的一条边都在AB上,首尾两个正方形各有一个顶点分别在AC、BC上,依次这样摆放上去,则最多能摆放![]()
![]() 个小正方形纸片.
个小正方形纸片.
A. 14个 B. 15个 C. 16个 D. 17个
【答案】C
【解析】分析:
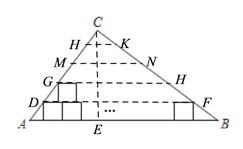
如下图,过点C作CE⊥AB于点E,则由已知条件易得CE=4.8,从而可知在△ABC内部,小正方形可以摆放4层,设这四层小正方形的上边沿所在直线分别与AC、BC相交于点D、F、G、H、M、N、K、H,则可得HK∥MN∥GH∥DF∥AB,由此结合已知条件求得DF、GH、MN、HK的长,即可知道每层可摆放的小正方形的个数,从而求得所求答案.
详解:
过点C作CE⊥AB于点E,
∵在Rt△ABC中,∠C=90°,AC=8,BC=6,
∴由勾股定理可得:AB=10,
∵S△ABC=![]() AB·CE=
AB·CE=![]() AC·BC,
AC·BC,
∴![]() ,解得CE=4.8,
,解得CE=4.8,
∴△ABC内部,小正方形可以摆放4层,
设这四层小正方形的上边沿所在直线分别与AC、BC相交于点D、F、G、H、M、N、K、H,则可得HK∥MN∥GH∥DF∥AB,
∵DF∥AB,小正方形的边长为1,
∴DF:AB=(4.8-1):4.8,解得DF=![]() ,
,
∴第一层可摆放小正方形7个,
同理可得第二层可摆放小正方形5个,第三层可摆放小正方形3个,第四层可摆放小正方形1个,
∴△ABC内部共可摆放小正方形16个.
故选C.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案【题目】某农机租赁公司共有50台收割机,其中甲型20台,乙型30台,现将这50台联合收割机派往A,B两地区收割水稻,其中30台派往A地区,20台派往B地区,两地区与该农机公司商定的每天租赁价格如表:
每台甲型收割机的租金 | 每台乙型收割机的租金 | |
A地区 | 1800元 | 1600元 |
B地区 | 1600元 | 1200元 |
![]() 设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y元,求y关于x的函数关系式;
设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y元,求y关于x的函数关系式;
![]() 若使农机租赁公司这50台收割机一天所获租金不低于79600元,试写出满足条件的所有分派方案;
若使农机租赁公司这50台收割机一天所获租金不低于79600元,试写出满足条件的所有分派方案;
![]() 农机租赁公司拟出一个分派方案,使该公司50台收割机每天获得租金最高,并说明理由.
农机租赁公司拟出一个分派方案,使该公司50台收割机每天获得租金最高,并说明理由.