题目内容
【题目】在△ABC中，AB=AC，BD=CD，∠BAD=40°，AD=AE．求∠CDE的度数．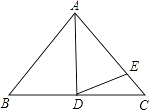 
【答案】解：∵AB=AC，
∴△ABC为等腰三角形，
∵AD=AE，
∴△ADE为等腰三角形，
∵∠BAD=40°，
∴∠DAE=40°，
∴∠ADE= 
（180°﹣∠DAE）= （180°﹣40°）=70°，
又∵△ABC为等腰三角形，BD=CD，
∴AD⊥CD（三线合一），
∴∠CDE=90°﹣∠ADE=90°﹣70°=20°．
故答案为：20°
【解析】首先得到△ABC，△ADE均为等腰三角形，再根据等腰三角形的性质求解．
【考点精析】通过灵活运用三角形的内角和外角，掌握三角形的三个内角中，只可能有一个内角是直角或钝角；直角三角形的两个锐角互余；三角形的一个外角等于和它不相邻的两个内角的和；三角形的一个外角大于任何一个和它不相邻的内角即可以解答此题．
智慧小复习系列答案
【题目】如果一个多边形的各边都相等，且各内角也都相等，那么这个多边形就叫做正多边形．如图，就是一组正多边形，观察每个正多边形中∠α的变化情况： 
（1）将下面的表格补充完整：
（2）根据规律，是否存在一个正多边形，其中的∠α=21°？若存在，请求出n的值，若不存在，请说明理由．
正多边形边数 | 3 | 4 | 5 | 6 | … | n |
∠α的度数 | 60° | … |
【题目】问题情景：
如图，在直角坐标系xOy中,点A、B为二次函数y=ax2(a>0)图象上的两点，且点A、B的横坐标分别为m、n(m>n>0),连接OA、AB、OB.设△AOB的面积为S时，解答下列问题:
探究：当a=1时，
mn | m | S | |
m=3,n=1 | 3 | 2 | |
m=5,n=2 | 10 | 3 |
当a=2时，
2mn | m | S | |
m=3,n=1 | 6 | 2 | |
m=5,n=2 | 20 | 3 |
归纳证明：
对任意m、n(m>n>0),猜想S=_________________ (用a,m,n表示)，并证明你的猜想.
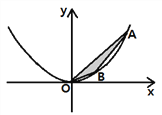
拓展应用：
若点A、B的横坐标分别为m、n(m>0>n),其它条件不变时，△AOB的面积S=____ (用a, m,n表示).
