题目内容
(2009•上海模拟)如果正方形ABCD的边长为1,圆A与以CD为半径的圆C相切,那么圆A的半径等于
-1或
+1
-1或
+1.
| 2 |
| 2 |
| 2 |
| 2 |
分析:根据题意画出图形,利用当圆A与以CD为半径的圆C相外切以及当圆A与以CD为半径的圆C相内切,分别求出即可.
解答:
 解:∵正方形ABCD的边长为1,圆A与以CD为半径的圆C相切,
解:∵正方形ABCD的边长为1,圆A与以CD为半径的圆C相切,
∴如图1,当圆A与以CD为半径的圆C相外切,
∵AC=
=
,BC=CD=FC=1,
AF+FC=AC,
∴AF=AC-FC=
-1,
如图2,当圆A与以CD为半径的圆C相内切,
∵AC=
=
,BC=CD=EC=1,
AC+EC=AE,
∴AE=AC+EC=
+1,
综上所述:圆A的半径等于
-1或
+1.
故答案为:
-1或
+1.

 解:∵正方形ABCD的边长为1,圆A与以CD为半径的圆C相切,
解:∵正方形ABCD的边长为1,圆A与以CD为半径的圆C相切,∴如图1,当圆A与以CD为半径的圆C相外切,
∵AC=
| 12+12 |
| 2 |
AF+FC=AC,
∴AF=AC-FC=
| 2 |
如图2,当圆A与以CD为半径的圆C相内切,
∵AC=
| 12+12 |
| 2 |
AC+EC=AE,
∴AE=AC+EC=
| 2 |
综上所述:圆A的半径等于
| 2 |
| 2 |
故答案为:
| 2 |
| 2 |
点评:此题主要考查了相切两圆的性质以及正方形的性质,根据已知进行分类讨论得出是解题关键.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
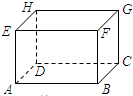 (2009•上海模拟)已知长方体ABCD-EFGH如图所示,那么下列直线中与直线AB异面的直线是( )
(2009•上海模拟)已知长方体ABCD-EFGH如图所示,那么下列直线中与直线AB异面的直线是( )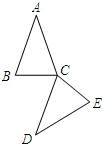 (2009•上海模拟)如图,在△ABC中,AB=AC,∠B=70°,将△ABC绕点C按逆时针方向旋转到△DEC处,使CD∥AB,那么旋转角等于
(2009•上海模拟)如图,在△ABC中,AB=AC,∠B=70°,将△ABC绕点C按逆时针方向旋转到△DEC处,使CD∥AB,那么旋转角等于