Question

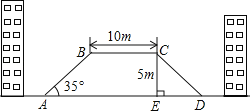
【题目】如图，为了缓解交通拥堵，方便行人，在某街道计划修建一座横断面为梯形ABCD的过街天桥，若天桥斜坡AB的坡角∠BAD为35°，斜坡CD的坡度为i=1：1.2（垂直高度CE与水平宽度DE的比），上底BC=10m，天桥高度CE=5m，求天桥下底AD的长度？（结果精确到0.1m，参考数据：sin35°≈0.57，cos35°≈0.82，tan35°≈0.70）

Answer 1

【答案】解：过B作BF⊥AD于F，则四边形BCEF为矩形，

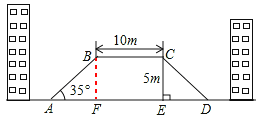
则BF=CE=5m，BC=EF=10m，

在Rt△ABF中，，

∴。

在Rt△CDE中，∵CD的坡度为i=1：1.2，

∴，即ED=6m。

∴AD=AF+EF+ED=7.14+10+6=23.14≈23.1（m）。

答：天桥下底AD的长度为23.1m。

【解析】

试题分析：过B作BF⊥AD于F，可得四边形BCEF为矩形，BF=CE，在Rt△ABF和Rt△CDE中，分别解直角三角形求出AF，ED的长度，继而可求得AD的长度。