题目内容
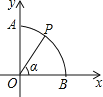
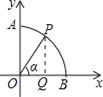
【题目】如图,以圆O为圆心,半径为1的弧交坐标轴于A,B两点,P是弧![]() 上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是
上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是
A. (sinα,sinα) B. (cosα,cosα) C. (cosα,sinα) D. (sinα,cosα)
【答案】C
【解析】过P作PQ⊥OB,交OB于点Q,在直角三角形OPQ中,利用锐角三角函数定义表示出OQ与PQ,即可确定出P的坐标.
解:过P作PQ⊥OB,交OB于点Q,
在Rt△OPQ中,OP=1,∠POQ=α,
∴sinα=![]() ,cosα=
,cosα=![]() ,即PQ=sinα,OQ=cosα,
,即PQ=sinα,OQ=cosα,
则P的坐标为(cosα,sinα),
故选C.
“点睛”此题考查了解直角三角形,以及坐标与图形性质,熟练掌握锐角三角函数定义是解本题的关键.

练习册系列答案
相关题目