Question

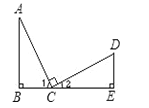
【题目】如图，在△ABC和△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，点C、D、E在同一直线上，连接BD．

（1）求证：BD=EC；

（2）BD与CE有何位置关系？请证你的猜想．

Answer 1

【答案】（1）证明见解析；(2) BD垂直于CE,理由见解析.

【解析】试题分析：(1)根据同角的余角相等得出∠BAD=∠CAE，结合已知条件得出△BAD和△CAE全等，从而得出答案；(2)根据全等得出∠ADB=∠AED，然后根据直角三角形的性质以及等量代换得出∠BDE=90°，从而得出垂直．

试题解析：(1)∵∠BAC=∠DAE=90°，∴∠BAD+∠CAD=∠CAE+∠CAD，

即∠BAD=∠CAE， ∵在△BAD和△CAE中，AB＝AC，∠BAD＝∠CAE，AD＝AE，

∴△BAD≌△CAE（SAS）， ∴BD=CE；

(2)∵△BAD≌△CAE，∴∠ADB=∠AED， ∵∠ADE+∠AED=90°，

∴∠ADE+∠ADB=90°，即∠BDE=90°，则BD⊥CE．