Question

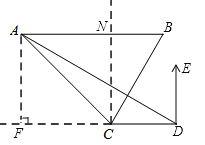
【题目】如图,海中两个灯塔A,B,其中B位于A的正东方向上,渔船跟踪鱼群由西向东航行,在点C处测得灯塔A在西北方向上,灯塔B在北偏东30°方向上,渔船不改变航向继续向东航行30海里到达点D,这时测得灯塔A在北偏西60°方向上,求灯塔A,B间的距离.(计算结果用根号表示,不取近似值)

Answer 1

【答案】灯塔A、B间的距离为(20+30)海里.

【解析】试题分析：过点A作AF⊥CD，垂足为F，过点D作DE⊥CD，可得出∠FCA=∠ACN=45°，∠NCB=30°，∠ADE=60°，则∠FAD=60°，∠FAC=∠FCA=45°，∠ADF=30°，从而AF=FC=AN=NC，设AF=FC=x，则tan30°=，解得x=，由tan30°=，得到，解得：BN=，由AB=AN+BN，即可得出结论．

试题解析：过点A作AF⊥CD，垂足为F，过点D作DE⊥CD，如图所示：由题意可得出：∠FCA=∠ACN=45°，∠NCB=30°，∠ADE=60°，则∠FAD=60°，∠FAC=∠FCA=45°，∠ADF=30°，∴AF=FC=AN=NC，设AF=FC=x，∴tan30°=，解得：x=，∵tan30°=，∴，解得：BN=，∴AB=AN+BN==．

答：灯塔A、B间的距离为（）海里．