题目内容
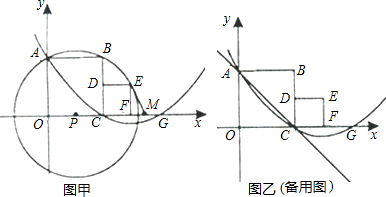
如图,分别以两个彼此相邻的正方形OABC与CDEF的边OC、OA所在直线为x轴、y轴建立平面直角坐标系(C、F两点在x轴正半轴上).若⊙P过A、B、E三点(圆心P在x轴上),抛物线y= x2+bx+c经过A、C两点,与x轴的另一交点为G,正方形CDEF的面积为4.
x2+bx+c经过A、C两点,与x轴的另一交点为G,正方形CDEF的面积为4.(1)求点B的坐标;
(2)求抛物线的解析式;
(3)设直线AC与抛物线对称轴交于点N,点Q是此对称轴上不与点N重合的一动点.
①求△ACQ周长的最小值;
②设点Q的纵坐标为t,△ACQ的面积为S,直接写出S与t之间的函数关系式,并指出相应的t的取值范围.

【答案】分析:(1)如图甲,连接PE、PB,设PC=n,由正方形CDEF的面积为4,可得CD=CF=2,根据圆和正方形的对称性知:OP=PC=n,由PB=PE,根据勾股定理即可求得n的值,继而求得B的坐标;
(2)由(1)知A(0,4),C(4,0),即可求得抛物线的解析式;
(3)①如图乙,延长AB交抛物线于A′,连CA′交对称轴x=6于Q,连AQ,则有AQ=A′Q,△ACQ周长的最小值为AC+A′C的长,利用勾股定理即可求得△ACQ周长的最小值;
②分别当Q点在F点上方时,当Q点在线段FN上时,当Q点在N点下方时去分析即可求得答案.
解答:解: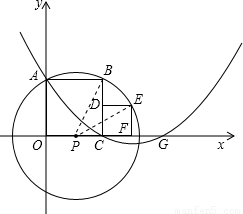 (1)如图,连接PE、PB,设PC=n,
(1)如图,连接PE、PB,设PC=n,
由正方形CDEF的面积为4,可得CD=CF=2,
根据圆和正方形的对称性知,OP=PC=n,
由PB=PE,根据勾股定理,得
PB2=BC2+PC2=4n2+n2=5n2,
PE2=PF2+EF2=(n+2)2+4,即5n2=(n+2)2+4
解得n1=2或n2=-1(舍去).
∴BC=OC=4,
故点B的坐标为(4,4);
(2)由(1)A(0,4),C(4,0),
∵抛物线y= x2+bx+c经过A、C两点,
x2+bx+c经过A、C两点,
∴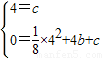
解得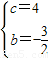 ,.
,.
∴抛物线的解析式为y= x2-
x2- x+4;
x+4;
(3)①如图,延长AB交抛物线于点A′,连接CA′交对称轴x=6于点Q,连接AQ,则有AQ=A′Q.△ACQ周长的最小值为AC+A′C的长.
利用勾股定理,在Rt△AOC中,AC=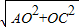 =4
=4 ,
,
在Rt△A′BC中,A′C=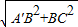 =4
=4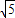 ,
,
即△ACQ周长的最小值为4 +4
+4 ;
;
②直线AC的解析式为x+y-4=0,当x=6时,y=-2,由于点Q与N不重合,
∴t≠-2,
当t>-2时,
Q点在F点上方时,S=S梯形ACFK-S△AKQ-S△CFQ= ×(6+2)×2-
×(6+2)×2- ×(4-t)×6-
×(4-t)×6- ×t×2=2t-4,
×t×2=2t-4,
同理,当t<-2时可得:当Q点在线段FN上时,S=-2t-4.
点评:此题考查了待定系数法求二次函数的解析式,圆的性质,相似三角形的判定与性质以及勾股定理等知识.此题综合性很强,题目难度较大,解题的关键是方程思想、分类讨论与数形结合思想的应用.
(2)由(1)知A(0,4),C(4,0),即可求得抛物线的解析式;
(3)①如图乙,延长AB交抛物线于A′,连CA′交对称轴x=6于Q,连AQ,则有AQ=A′Q,△ACQ周长的最小值为AC+A′C的长,利用勾股定理即可求得△ACQ周长的最小值;
②分别当Q点在F点上方时,当Q点在线段FN上时,当Q点在N点下方时去分析即可求得答案.
解答:解:
 (1)如图,连接PE、PB,设PC=n,
(1)如图,连接PE、PB,设PC=n,由正方形CDEF的面积为4,可得CD=CF=2,
根据圆和正方形的对称性知,OP=PC=n,
由PB=PE,根据勾股定理,得
PB2=BC2+PC2=4n2+n2=5n2,
PE2=PF2+EF2=(n+2)2+4,即5n2=(n+2)2+4
解得n1=2或n2=-1(舍去).
∴BC=OC=4,
故点B的坐标为(4,4);
(2)由(1)A(0,4),C(4,0),
∵抛物线y=
 x2+bx+c经过A、C两点,
x2+bx+c经过A、C两点,∴
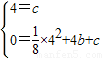
解得
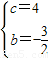 ,.
,.∴抛物线的解析式为y=
 x2-
x2- x+4;
x+4;(3)①如图,延长AB交抛物线于点A′,连接CA′交对称轴x=6于点Q,连接AQ,则有AQ=A′Q.△ACQ周长的最小值为AC+A′C的长.
利用勾股定理,在Rt△AOC中,AC=
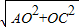 =4
=4 ,
,在Rt△A′BC中,A′C=
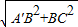 =4
=4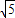 ,
,即△ACQ周长的最小值为4
 +4
+4 ;
;②直线AC的解析式为x+y-4=0,当x=6时,y=-2,由于点Q与N不重合,
∴t≠-2,
当t>-2时,
Q点在F点上方时,S=S梯形ACFK-S△AKQ-S△CFQ=
 ×(6+2)×2-
×(6+2)×2- ×(4-t)×6-
×(4-t)×6- ×t×2=2t-4,
×t×2=2t-4,同理,当t<-2时可得:当Q点在线段FN上时,S=-2t-4.
点评:此题考查了待定系数法求二次函数的解析式,圆的性质,相似三角形的判定与性质以及勾股定理等知识.此题综合性很强,题目难度较大,解题的关键是方程思想、分类讨论与数形结合思想的应用.

练习册系列答案
相关题目
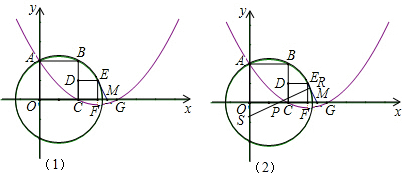
 (圆心P在x轴上),抛物线y=
(圆心P在x轴上),抛物线y= (圆心P在x轴上),抛物线y=
(圆心P在x轴上),抛物线y= x2+bx+c经过A、C两点,与x轴的另一交点为G,正方形CDEF的面积为4.
x2+bx+c经过A、C两点,与x轴的另一交点为G,正方形CDEF的面积为4.