题目内容
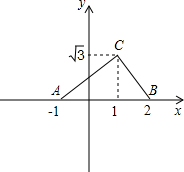
如图，在平面直角坐标系中，Rt△ABC各点坐标分别为A（-1，0），B（2，0），C（1，
），∠C=90°．
（1）求△ABC的面积．
（2）把△ABC向右平移三个单位，画出平移后的△A′B′C′，并写出各点坐标．
（3）求出∠CBC′的度数．
| 3 |
（1）求△ABC的面积．
（2）把△ABC向右平移三个单位，画出平移后的△A′B′C′，并写出各点坐标．
（3）求出∠CBC′的度数．
（1）∵A（-1，0）B（2，0）C（1，
）
∴AB=3，AB边上的高位
，
∴S△ABC=
×3×
=
；
（2）作图如下：
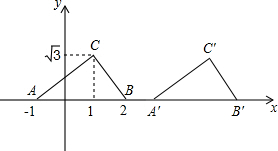
A'（2，0）B'（5，0）C'（4，
）…（6分）（两个正确只得1分）
（3）∵由平移可知AC∥A'C'
∴∠CBC′=∠ACB=90°…（8分）
| 3 |
∴AB=3，AB边上的高位
| 3 |
∴S△ABC=
| 1 |
| 2 |
| 3 |
3
| ||
| 2 |
（2）作图如下：
A'（2，0）B'（5，0）C'（4，
| 3 |
（3）∵由平移可知AC∥A'C'
∴∠CBC′=∠ACB=90°…（8分）
练习册系列答案
阅读快车系列答案
相关题目
