题目内容
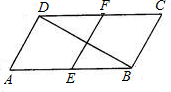 已知如图所示,在平行四边形ABCD中,∠A=60°,E、F分别是AB、CD的中点,且AB=2AD.
已知如图所示,在平行四边形ABCD中,∠A=60°,E、F分别是AB、CD的中点,且AB=2AD.
(1)求证:BD= EF;
EF;
(2)试判断EF与BD的位置关系.
(1)证明:如图,连接DE.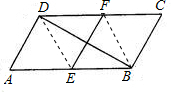
∵AB=2AD,E是AB的中点,
∴AD=AE,
又∠A=60°,
∴△ADE是等边三角形,
∴DE=AE=BE,
∴△ABD是直角三角形,
∴∠ADB=90°,又∠A=60°,
∴∠ABD=90°-60°=30°,
∴AB=2AD,
∴BD= AD,
AD,
∵DF∥AE,DF=AE,
∴四边形AEFD是平行四边形,
∴BD= EF;
EF;
(2)解:EF与BD互相垂直平分.理由如下:
连结BF,如图,
∵平行四边形ABCD中,E、F分别是AB、CD的中点,
∴DF∥BE,DF∥BE,
∴四边形BEDF为平行四边形,
根据(1)中的结论,
∵四边形AEFD是平行四边形,△ABD是直角三角形,
∴AD⊥DB,而E点为AB的中点,
∴DE=BE,
∴四边形BEDF为菱形,
∴EF与BD互相垂直平分.
分析:(1)由已知不难发现:EF=AD,故要证明结论,只需证明△ADB是直角三角形即可.
(2)结合第(1)小题的结论,不难发现它们的位置关系是垂直平分的.
点评:特别注意等边三角形的判定:有一个角是60°的等腰三角形是等边三角形.直角三角形的判定:三角形一边上的中线等于这条边的一半,则该三角形是直角三角形.

∵AB=2AD,E是AB的中点,
∴AD=AE,
又∠A=60°,
∴△ADE是等边三角形,
∴DE=AE=BE,
∴△ABD是直角三角形,
∴∠ADB=90°,又∠A=60°,
∴∠ABD=90°-60°=30°,
∴AB=2AD,
∴BD=
 AD,
AD,∵DF∥AE,DF=AE,
∴四边形AEFD是平行四边形,
∴BD=
 EF;
EF;(2)解:EF与BD互相垂直平分.理由如下:
连结BF,如图,
∵平行四边形ABCD中,E、F分别是AB、CD的中点,
∴DF∥BE,DF∥BE,
∴四边形BEDF为平行四边形,
根据(1)中的结论,
∵四边形AEFD是平行四边形,△ABD是直角三角形,
∴AD⊥DB,而E点为AB的中点,
∴DE=BE,
∴四边形BEDF为菱形,
∴EF与BD互相垂直平分.
分析:(1)由已知不难发现:EF=AD,故要证明结论,只需证明△ADB是直角三角形即可.
(2)结合第(1)小题的结论,不难发现它们的位置关系是垂直平分的.
点评:特别注意等边三角形的判定:有一个角是60°的等腰三角形是等边三角形.直角三角形的判定:三角形一边上的中线等于这条边的一半,则该三角形是直角三角形.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
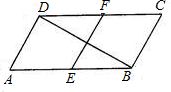 已知如图所示,在平行四边形ABCD中,∠A=60°,E、F分别是AB、CD的中点,且AB=2AD.
已知如图所示,在平行四边形ABCD中,∠A=60°,E、F分别是AB、CD的中点,且AB=2AD.

