题目内容
 如图,D、E分别为△ABC的边AB、AC上的点,且DE∥BC,将△ABC沿DE所在直线折叠,点A落在BC边上的点F处,∠B=42°,则∠BDF的度数为
如图,D、E分别为△ABC的边AB、AC上的点,且DE∥BC,将△ABC沿DE所在直线折叠,点A落在BC边上的点F处,∠B=42°,则∠BDF的度数为
- A.96°
- B.79°
- C.48°
- D.42°
A
分析:先根据图形翻折不变性的性质可得∠ADE=∠EDF,再由平行线的性质可得∠B=∠ADE=42°,最后由平角的性质即可求解.
解答:∵△DEF是△DEA沿直线DE翻折变换而来,
∴∠ADE=∠EDF,
∵DE∥BC,∠B=42°,
∴∠B=∠ADE=42°,
∴∠ADE=∠EDF=42°,
∴∠BDF=180°-∠ADE-∠EDF=180°-42°-42°=96°.
故选A.
点评:本题考查的是图形翻折变换的性质及平行线的性质,熟知折叠的性质是解答此题的关键.
分析:先根据图形翻折不变性的性质可得∠ADE=∠EDF,再由平行线的性质可得∠B=∠ADE=42°,最后由平角的性质即可求解.
解答:∵△DEF是△DEA沿直线DE翻折变换而来,
∴∠ADE=∠EDF,
∵DE∥BC,∠B=42°,
∴∠B=∠ADE=42°,
∴∠ADE=∠EDF=42°,
∴∠BDF=180°-∠ADE-∠EDF=180°-42°-42°=96°.
故选A.
点评:本题考查的是图形翻折变换的性质及平行线的性质,熟知折叠的性质是解答此题的关键.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案
相关题目
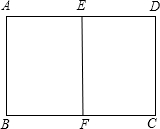 如图,E,F分别为矩形ABCD的边AD,BC的中点,若矩形ABCD∽矩形EABF,AB=1.求矩形ABCD
如图,E,F分别为矩形ABCD的边AD,BC的中点,若矩形ABCD∽矩形EABF,AB=1.求矩形ABCD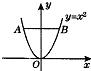 5、如图,A、B分别为y=x2上两点,且线段AB⊥y轴,若AB=6,则直线AB的表达式为( )
5、如图,A、B分别为y=x2上两点,且线段AB⊥y轴,若AB=6,则直线AB的表达式为( )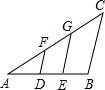 如图,D,E分别为AB的三等分点,DF∥EG∥BC,若BC=12,则DF=
如图,D,E分别为AB的三等分点,DF∥EG∥BC,若BC=12,则DF= 如图,D、E分别为⊙O半径OA、OB的中点,C是
如图,D、E分别为⊙O半径OA、OB的中点,C是
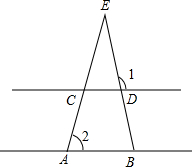 (2012•朝阳)如图,C、D分别为EA、EB的中点,∠E=30°,∠1=110°,则∠2的度数为( )
(2012•朝阳)如图,C、D分别为EA、EB的中点,∠E=30°,∠1=110°,则∠2的度数为( )