题目内容
【题目】如图,一艘轮船从A处向正北方向航行,达到B处后,继续航行到达D处时发现,灯塔C恰好在正西方向,从A处、B处望灯塔C的角度分别是∠A=30°,∠DBC=60°,若DB等于36海里,求B到CA的距离.
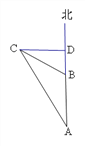
【答案】B到CA的距离等于36海里.
【解析】试题分析:由三角形外角的性质得∠BCA=30°,由直角三角形的两个锐角互余得∠BCD=30°,由此得∠BCA = ∠BCD,CB平分∠ACD,由角平分线的性质得B到CA的距离等于36海里.
试题解析:∵C在D的正西方向,
∴∠CDB=90°,
∵∠DBC =∠BCA +∠A,
∴∠BCA =∠DBC -∠A=60°-30°=30°,
在Rt△BCD中,
∠BCD+∠CBD=90°,
∴∠BCD= 90°-∠CBD=90°-60°=30°,
∴∠BCA = ∠BCD,
∴ CB平分∠ACD,
∴B到CA的距离等于BD=36海里.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目