题目内容
【题目】如图,长方形ABCD中,∠DAB=∠B=∠C=∠D=90°,AD=BC=8,AB=CD=17.点E为射线DC上的一个动点,△ADE与△AD′E关于直线AE对称,当△AD′B为直角三角形时,DE的长为______.
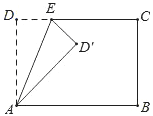
【答案】2或32.
【解析】分两种情况:点E在DC线段上,点E为DC延长线上的一点,进一步分析探讨得出答案即可.
解:如图1,
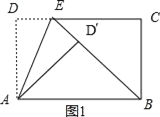
∵折叠,∴△AD′E≌△ADE,∴∠AD′E=∠D=90°,∵∠AD′B=90°,∴B、D′、E三点共线,
又∵ABD′∽△BEC,AD′=BC,∴ABD′≌△BEC,∴BE=AB=17,
∵BD′=![]() =15,
=15,
∴DE=D′E=17﹣15=2;
如图2,
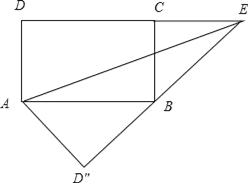
∵∠ABD″+∠CBE=∠ABD″+∠BAD″=90°,
∴∠CBE=∠BAD″,
在△ABD″和△BEC中,
∠D″=∠BCE,AD″=BC,∠CBE=∠BAD″,
∴△ABD″≌△BEC,
∴BE=AB=17,
∴DE=D″E=17+15=32.
综上所知,DE=2或32.
故答案为:2或32.
“点睛”翻折的性质,三角形全等的判定与性质,勾股定理,掌握翻折的性质,分类探讨的思想方法是解决问题的关键.

练习册系列答案
相关题目