题目内容
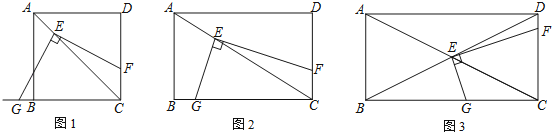
【题目】（1）如图1，将直角的顶点E放在正方形ABCD的对角线AC上，使角的一边交CD于点F，另一边交CB或其延长线于点G，求证：EF=EG；
（2）如图2，将（1）中的“正方形ABCD”改成“矩形ABCD”，其他条件不变．若AB=m，BC=n，试求
的值；
（3）如图3，将直角顶点E放在矩形ABCD的对角线交点，EF、EG分别交CD与CB于点F、G，且EC平分∠FEG．若AB=2，BC=4，求EG、EF的长．
考点：四边形综合题．
【答案】
【解析】
试题分析:（1）首先过点E分别作BC、CD的垂线，垂足分别为H、P，然后利用ASA证得Rt△FEP≌Rt△GEH，则问题得证；
（2）首先过点E分别作BC、CD的垂线，垂足分别为M、N，易证得EM∥AB，EN∥AD，则可证得△CEN∽△CAD，△CEM∽△CAB，又由有两角对应相等的三角形相似，证得△GME∽△FNE，根据相似三角形的对应边成比例，即可求得答案；
（3）过点E作EM⊥BC于M，过点E作EN⊥CD于N，垂足分别为M、N，过点C作CP⊥EG交EG的延长线于点P，过点C作CQ⊥EF垂足为Q，可得四边形EPCQ是矩形，四边形EMCN是矩形，可得EC平分∠FEG，可得矩形EPCQ是正方形，然后易证△PCG≌△QCF（AAS），进而可得：CG=CF，由（2）知：
=
=2，进而可得：EF=2EG，然后易证EM和EN分别是△ABC和△BCD的中位线，进而可得：EM=1，EN=2，MC=2，CN=1，然后易证△EMG∽△ENF，进而可得
，即NF=2MG，然后设MG=x，根据CG=CF，列出方程即可解出x的值，即MG的值，然后在Rt△EMG中，由勾股定理即可求出EG的值，进而可得EF的值．
（1）证明：如图1，过点E作EH⊥BC于H，过点E作EP⊥CD于P，
∵四边形ABCD为正方形，
∴CE平分∠BCD，
又∵EH⊥BC，EP⊥CD，
∴EH=EP，
∴四边形EHCP是正方形，
∴∠HEP=90°，
∵∠GEH+∠HEF=90°，∠PEF+∠HEF=90°，
∴∠PEF=∠GEH，
∴Rt△FEP≌Rt△GEH，
∴EF=EG；
（2）解：如图2，过点E作EM⊥BC于M，过点E作EN⊥CD于N，垂足分别为M、N，
则∠MEN=90°，
∴EM∥AB，EN∥AD．
∴△CEN∽△CAD，△CEM∽△CAB，
∴
，
，
∴
，
即
．
∴
，
∴
；
（3）解：如图3，
过点E作EM⊥BC于M，过点E作EN⊥CD于N，垂足分别为M、N，
过点C作CP⊥EG交EG的延长线于点P，过点C作CQ⊥EF垂足为Q，
则四边形EPCQ是矩形，四边形EMCN是矩形，
∵EC平分∠FEG，
∴CQ=CP，
∴矩形EPCQ是正方形，
∴∠QCP=90°，
∴∠QCG+∠PCG=90°，
∵∠QCG+∠QCF=90°，
∴∠PCG=∠QCF，
在△PCG和△QCF中，
，
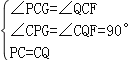∴△PCG≌△QCF（AAS），
∴CG=CF，
由（2）知：
=
，
∵BC=4，AB=2，
∴==2，
∴EF=2EG，
∵点E放在矩形ABCD的对角线交点，
∴EM和EN分别是△ABC和△BCD的中位线，
∴EM=
AB=1，EN=AD=
=2，MC=
，CN=
，
∵四边形EMCN是矩形，
∴∠NEM=90°，
∴∠MEG+∠GEN=90°，
∵∠GEF=90°，
∴∠FEN+∠GEN=90°，
∴∠MEG=∠FEN，
∵∠EMG=∠FNE=90°，
∴△EMG∽△ENF，
∴
，
即NF=2MG，
设MG=x，则NF=2x，CG=2﹣x，CF=1+2x，
∵CG=CF，
∴2﹣x=1+2x，
解得：x=
，
∴MG=，
在Rt△EMG中，由勾股定理得：
EG=
=
，
∵EF=2EG，
∴EF=
．
