Question

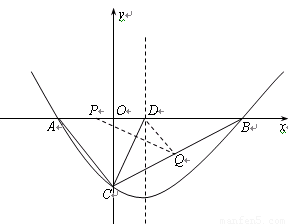
已知抛物线y＝ax²＋bx＋c（a＞0）的图象经过点B（14,0）和C（0，－8），对称轴为x＝4．

（1）求该抛物线的解析式；

（2）点D在线段AB上且AD＝AC，若动点P从A出发沿线段AB以每秒1个单位长度的速度匀速运动，同时另一动点Q以某一速度从C出发沿线段CB匀速运动，问是否存在某一时刻，使线段PQ被直线CD垂直平分？若存在，请求出此时的时间t（秒）和点Q的运动速度；若不存在，请说明理由；

（3）在（2）的结论下，直线x＝1上是否存在点M使△MPQ为等腰三角形？若存在，请求出所有点M的坐标，若不存在，请说明理由．

 

Answer 1

【答案】

（1）；  

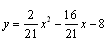（2）存在，理由如下：

综上所述：存在5个M点，即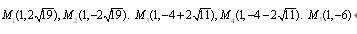

【解析】（1）由题意抛物线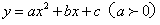的图象经过点B（14，0）和C（0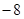，），对称轴为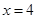，根据待定系数法可以求得该抛物线的解析式；

（2）假设存在，设出时间t，则根据线段PQ被直线CD垂直平分，再由垂直平分线的性质及勾股定理来求解t，看t是否存在；

（3）假设直线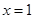上是存在点M，使△MPQ为等腰三角形，此时要分三种情况讨论：①当PQ为等腰△MPQ的腰时，且P为顶点；②当PQ为等腰△MPQ的腰时，且Q为顶点；②当PM为等腰△MPQ的腰时，且M为顶点；然后再根据等腰三角形的性质及直角三角形的勾股定理求出M点坐标．