题目内容
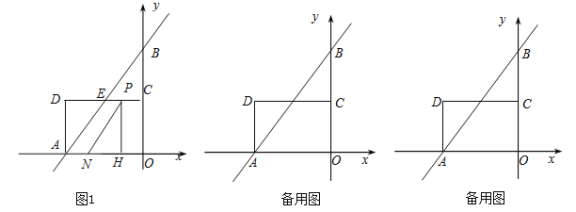
【题目】如图1,在平面直角坐标系中,直线![]() 分别交x轴,y轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形(有一个角是直角的平行四边形).
分别交x轴,y轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形(有一个角是直角的平行四边形).
(1)直接写出点A,B的坐标,并求直线AB与CD交点E的坐标;
(2)动点P从点C出发,沿线段CD以每秒1个单位长度的速度向终点D运动;同时动点N从点A出发,沿线段AO以每秒1个单位长度的速度向终点O运动,过点P作PHOA,垂足为H,连接NP.设点P的运动时间为t秒.
①若△NPH的面积为1,求t的值;
②点Q是点B关于点A的对称点,问BPPHHQ是否有最小值,如果有,直接写出相应的点P的坐标;如果没有,请说明理由.
【答案】(1)A(﹣3,0),B(0,4),E(﹣1.5,2);(2)①t=1或2;(2)P(﹣2,2).
【解析】
(1)分别令x与y等于0,即可求出点A与点B的坐标,由四边形AOCD为矩形,可知:CD∥x轴,进而可知:D、C、E三点的纵坐标相同,由点C为OB的中点,可求点C的坐标,然后将点C的纵坐标代入直线y=![]() x+4即可求直线AB与CD交点E的坐标;
x+4即可求直线AB与CD交点E的坐标;
(2)①分两种情况讨论,第一种情况:当0<t<2时;第二种情况:当2<t≤6时;
②由点Q是点B关于点A的对称点,先求出点Q的坐标,然后连接PB,CH,可得四边形PHCB是平行四边形,进而可得:PB=CH,进而可将BP+PH+HQ转化为CH+HQ+2,然后根据两点之间线段最短可知:当点C,H,Q在同一直线上时,CH+HQ的值最小,然后求出直线CQ的关系式,进而可求出直线CQ与x轴的交点H的坐标,从而即可求出点P的坐标
(1)∵直线y=![]() x+4分别交x轴,y轴于A,B两点,
x+4分别交x轴,y轴于A,B两点,
∴令x=0得:y=4,
令y=0得:x=-3,
∴A(-3,0),B(0,4),
∴OA=3,OB=4,
∵点C为OB的中点,
∴OC=2,
∴C(0,2),
∵四边形AOCD为矩形,
∴OA=CD=3,OC=AD=2,CD∥OA(x轴),
∴D、C、E三点的纵坐标相同,
∴点E的纵坐标为2,将y=2代入直线y=![]() x+4得:x=-1.5,
x+4得:x=-1.5,
∴E(-1.5,2);
(2)①分两种情况讨论:
第一种情况当0≤t<1.5时,如图1,
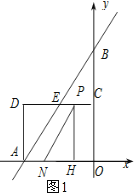
根据题意可知:经过t秒,CP=t,AN=t,HO=CP=t,PH=OC=2,
∴NH=3-2t,
∵S△NPH=![]() PHNH,且△NPH的面积为1,
PHNH,且△NPH的面积为1,
∴![]() ×2×(3-2t)=1,
×2×(3-2t)=1,
解得:t=1;
第二种情况:当1.5≤t≤3时,如图2,
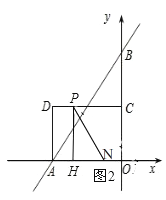
根据题意可知:经过t秒,CP=t,AN=t,HO=CP=t,PH=OC=2,
∴AH=3-t,
∴HN=AN-AH=t-(3-t)=2t-3,
∵S△NPH=![]() PHNH,且△NPH的面积为1,
PHNH,且△NPH的面积为1,
∴![]() ×2×(2t-3)=1,
×2×(2t-3)=1,
解得:t=2;
∴当t=1或2时,存在△NPH的面积为1;
②BP+PH+HQ有最小值,
连接PB,CH,HQ,则四边形PHCB是平行四边形,如图3,
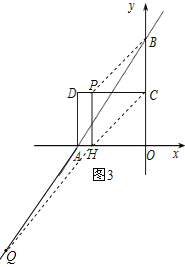
∵四边形PHCB是平行四边形,
∴PB=CH,
∴BP+PH+HQ=CH+HQ+2,
∵BP+PH+HQ有最小值,即CH+HQ+2有最小值,
∴只需CH+HQ最小即可,
∵两点之间线段最短,
∴当点C,H,Q在同一直线上时,CH+HQ的值最小,
过点Q作QM⊥y轴,垂足为M,
∵点Q是点B关于点A的对称点,
∴OA是△BQM的中位线,
∴QM=2OA=6,OM=OB=4,
∴Q(-6,-4),
设直线CQ的关系式为:y=kx+b,
将C(0,2)和Q(-6,-4)分别代入上式得:
![]() ,
,
解得:![]() ,
,
∴直线CQ的关系式为:y=x+2,
令y=0得:x=-2,
∴H(-2,0),
∵PH∥y轴,
∴P(-2,2).

 53随堂测系列答案
53随堂测系列答案【题目】某商场用14500元购进甲、乙两种矿泉水共500箱,矿泉水的成本价与销售价如表(二)所示:
类别 | 成本价(元/箱) | 销售价(元/箱) |
甲 | 25 | 35 |
乙 | 35 | 48 |
求:(1)购进甲、乙两种矿泉水各多少箱?
(2)该商场售完这500箱矿泉水,可获利多少元?