题目内容
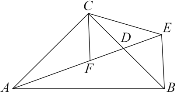
【题目】如图,![]() 是反比例函数
是反比例函数![]() 在第一象限图象上一点,点
在第一象限图象上一点,点![]() 的坐标为
的坐标为![]() .
.

![]() 当点
当点![]() 的横坐标逐渐增大时,
的横坐标逐渐增大时,![]() 的面积将如何变化?
的面积将如何变化?
![]() 若
若![]() 与
与![]() 均为直角三角形,其中
均为直角三角形,其中![]() ,求此反比例函数的解析式及点
,求此反比例函数的解析式及点![]() 的坐标.
的坐标.
【答案】(1)点![]() 的横坐标逐渐增大时,其纵坐标逐渐减小,则
的横坐标逐渐增大时,其纵坐标逐渐减小,则![]() 的面积将逐渐减小.(2)
的面积将逐渐减小.(2)![]() .
.
【解析】
作辅助线,可得出面积的表达式,由k的取值范围可以得出结论;
当若![]() 与
与![]() 均为直角三角形,其中
均为直角三角形,其中![]() 时,可先求得函数解析式,又因为特殊直角三角形可得出相应点的坐标.
时,可先求得函数解析式,又因为特殊直角三角形可得出相应点的坐标.
解:![]() 过
过![]() 作
作![]() ,垂足为
,垂足为![]() ,
,
设![]() ,
,
∵![]() 在第一象限,
在第一象限,
∴![]() 的面积
的面积![]() .
.
又∵当![]() 时,在每一个象限内,
时,在每一个象限内,![]() 随
随![]() 的增大而减小.
的增大而减小.
故当点![]() 的横坐标逐渐增大时,其纵坐标逐渐减小,则
的横坐标逐渐增大时,其纵坐标逐渐减小,则![]() 的面积将逐渐减小.
的面积将逐渐减小.
![]() 因为
因为![]() 是直角三角形,
是直角三角形,
所以![]() ,
,![]() ,
,
所以![]() .
.
代入![]() ,得
,得![]() ,
,
所以反比例函数的解析式为![]() .
.
∵![]() 为直角三角形,
为直角三角形,![]() ,
,
∴![]() 轴,设
轴,设![]() ,
,
则![]() ,
,![]() ,
,
所以![]() .
.
∵![]() 在反比例函数的图象上,
在反比例函数的图象上,
∴代入![]() ,得
,得![]() ,
,
化简得![]()
解得:![]() .
.
∵![]() ,
,
∴![]() .∴
.∴![]() ,
,
∴![]() ,
,
所以点![]() 的坐标为
的坐标为![]() .
.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目