题目内容
【题目】如图在平面直角坐标系中,O 是坐标原点,长方形 OACB 的顶点 A,B 分别在 x,y 轴上,已知 OA=3, 点 D 为 y 轴上一点,其坐标为(0,1),CD=5,点 P 从点 A 出发以每秒 1 个单位的速度沿线段 A﹣C﹣B 的方向运动,当点 P 与点 B 重合时停止运动,运动时间为 t 秒
(1)求 B,C 两点坐标;
(2)①求△OPD 的面积 S 关于 t 的函数关系式;
②当点 D 关于 OP 的对称点 E 落在 x 轴上时,求点 E 的坐标;
(3)在(2)②情况下,直线 OP 上求一点 F,使 FE+FA 最小.
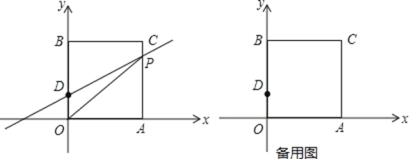
【答案】(1) B(0,5),C(3,5);(2)①S=-![]() t+4(t≥0);②(1,10);(3)见解析.
t+4(t≥0);②(1,10);(3)见解析.
【解析】
(1)由四边形OACB是矩形,得到BC=OA=3,在Rt△BCD中,由勾股定理得到BD=![]() =4,OB=5,从而求得点的坐标;
=4,OB=5,从而求得点的坐标;
(2)①当点P在AC上时,OD=1,BC=3,S=![]() ,当点在BC上时,OD=1,BP=5+3-t=8-t,得到S=
,当点在BC上时,OD=1,BP=5+3-t=8-t,得到S=![]() ×1×(8-t)=-
×1×(8-t)=-![]() t+4;
t+4;
②当点D关于OP的对称点落在x轴上时,得到点D的对称点是(1,0),求得E(1,0);
(3)由点D、E关于OP对称,连接AD交OP于F,找到点F,从而确定AD的长度就是AF+EF的最小值,在Rt△AOD中,由勾股定理求得AD=![]() ,即AF+EF的最小值=
,即AF+EF的最小值=![]() .
.
(1)如图1,
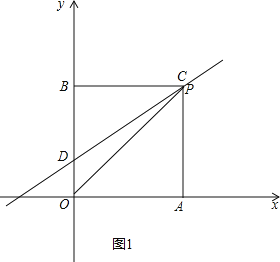
∵四边形OACB是矩形,
∴BC=OA=3,
在Rt△BCD中,∵CD=5,BC=3,
∴BD=![]() =4,
=4,
∴OB=5,
∴B(0,5),C(3,5);
(2)①当点P在AC上时,OD=1,BC=3,
∴S=![]() ,
,
当点在BC上时,OD=1,BP=5+3-t=8-t,
∴S=![]() ×1×(8-t)=-
×1×(8-t)=-![]() t+4;(t≥0)
t+4;(t≥0)
②当点D关于OP的对称点落在x轴上时,点D的对称点是(1,0),
∴E(1,0);
(3)如图2
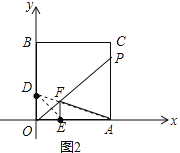
∵点D、E关于OP对称,连接AD交OP于F,
则AD的长度就是AF+EF的最小值,则点F即为所求.

 习题精选系列答案
习题精选系列答案【题目】中华文明,源远流长:中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 20 | 0.10 |
70≤x<80 | 30 | b |
80≤x<90 | a | 0.30 |
90≤x≤100 | 80 | 0.40 |
请根据所给信息,解答下列问题:
(1)a= , b=;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人? 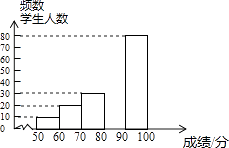
【题目】随着地铁和共享单车的发展,“地铁+单车”已成为很多市民出行的选择,李华从文化宫站出发,先乘坐地铁,准备在离家较近的A,B,C,D,E中的某一站出地铁,再骑共享单车回家,设他出地铁的站点与文化宫距离为x(单位:千米),乘坐地铁的时间y1(单位:分钟)是关于x的一次函数,其关系如下表:
地铁站 | A | B | C | D | E |
x(千米) | 8 | 9 | 10 | 11.5 | 13 |
y1(分钟) | 18 | 20 | 22 | 25 | 28 |
(1)求y1关于x的函数表达式;
(2)李华骑单车的时间(单位:分钟)也受x的影响,其关系可以用y2= ![]() x2﹣11x+78来描述,请问:李华应选择在那一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间.
x2﹣11x+78来描述,请问:李华应选择在那一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间.