题目内容
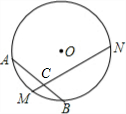 已知:如图,M是
已知:如图,M是 |
| AB |
| 3 |
(1)求圆心O到弦MN的距离;
(2)求∠ACM的度数.
分析:(1)连接OM,作OD⊥MN于D.根据垂径定理和勾股定理求解;
(2)根据(1)中的直角三角形的边求得∠M的度数.再根据垂径定理的推论发现OM⊥AB,即可解决问题.
(2)根据(1)中的直角三角形的边求得∠M的度数.再根据垂径定理的推论发现OM⊥AB,即可解决问题.
解答: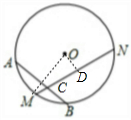 解:(1)连接OM,
解:(1)连接OM,
∵点M是
的中点,
∴OM⊥AB,
过点O作OD⊥MN于点D,
由垂径定理,得MD=
MN=2
,
在Rt△ODM中,OM=4,MD=2
,
∴OD=
=2,
故圆心O到弦MN的距离为2cm;
(2)cos∠OMD=
=
,
∴∠OMD=30°,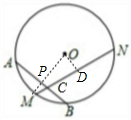
∵M为弧AB中点,OM过O,
∴AB⊥OM,
∴∠MPC=90°,
∴∠ACM=60°.
 解:(1)连接OM,
解:(1)连接OM,∵点M是
 |
| AB |
∴OM⊥AB,
过点O作OD⊥MN于点D,
由垂径定理,得MD=
| 1 |
| 2 |
| 3 |
在Rt△ODM中,OM=4,MD=2
| 3 |
∴OD=
| OM2-MD2 |
故圆心O到弦MN的距离为2cm;
(2)cos∠OMD=
| MD |
| OM |
| ||
| 2 |
∴∠OMD=30°,

∵M为弧AB中点,OM过O,
∴AB⊥OM,
∴∠MPC=90°,
∴∠ACM=60°.
点评:此题要能够熟练运用垂径定理和勾股定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
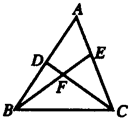 32、已知,如图,D是AB上一点,E是AC上的一点,BE,CD相交于点F,∠A=62°,∠ACD=35°,∠ABE=20°,求:
32、已知,如图,D是AB上一点,E是AC上的一点,BE,CD相交于点F,∠A=62°,∠ACD=35°,∠ABE=20°,求: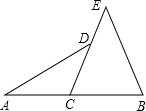 已知:如图,C是AB的中点,∠ADC=∠BEC,求证:AD=BE.
已知:如图,C是AB的中点,∠ADC=∠BEC,求证:AD=BE. (2012•房山区一模)已知:如图,M是AB的中点,以AM为直径的⊙O与BP相切于点N,OP∥MN.
(2012•房山区一模)已知:如图,M是AB的中点,以AM为直径的⊙O与BP相切于点N,OP∥MN. 已知:如图,D是AB上一点,E是AC上的一点,BE、CD相交于点F,∠A=62°,∠ACD=35°,∠ABE=20°.求:(1)∠BDC的度数; (2)∠BFD的度数.
已知:如图,D是AB上一点,E是AC上的一点,BE、CD相交于点F,∠A=62°,∠ACD=35°,∠ABE=20°.求:(1)∠BDC的度数; (2)∠BFD的度数.