题目内容
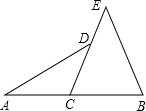 已知:如图,C是AB的中点,∠ADC=∠BEC,求证:AD=BE.
已知:如图,C是AB的中点,∠ADC=∠BEC,求证:AD=BE.分析:延长DC到F,使FC=DC,连接FB,由C为AC的中点,得到AC=BC,再由一对对顶角相等,利用SAS可得出三角形ADC与三角形FBC全等,由全等三角形的对应边相等得到AD=BF,全等三角形的对应角相等得到∠ADC=∠CFB,再由∠ADC=∠BEC,得到∠BEC=∠CFB,利用等角对等边得到EB=FB,等量代换可得出AD=BE,得证.
解答: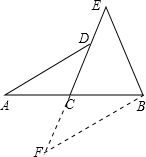 证明:延长DC到F,使FC=DC,连接FB,
证明:延长DC到F,使FC=DC,连接FB,
又C是AB的中点,∴AC=BC,
在△ADC和△BFC中,
,
∴△ADC≌△BFC(SAS),
∴AD=BF,∠ADC=∠CFB,
∵∠ADC=∠BEC,
∴∠CFB=∠BEC,
∴BE=BF,
∴AD=BE.
 证明:延长DC到F,使FC=DC,连接FB,
证明:延长DC到F,使FC=DC,连接FB,又C是AB的中点,∴AC=BC,
在△ADC和△BFC中,
|
∴△ADC≌△BFC(SAS),
∴AD=BF,∠ADC=∠CFB,
∵∠ADC=∠BEC,
∴∠CFB=∠BEC,
∴BE=BF,
∴AD=BE.
点评:此题考查了全等三角形的判定与性质,以及等腰三角形的判定与性质,熟练掌握判定与性质是解本题的关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
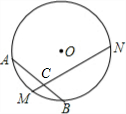 已知:如图,M是
已知:如图,M是
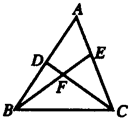 32、已知,如图,D是AB上一点,E是AC上的一点,BE,CD相交于点F,∠A=62°,∠ACD=35°,∠ABE=20°,求:
32、已知,如图,D是AB上一点,E是AC上的一点,BE,CD相交于点F,∠A=62°,∠ACD=35°,∠ABE=20°,求: (2012•房山区一模)已知:如图,M是AB的中点,以AM为直径的⊙O与BP相切于点N,OP∥MN.
(2012•房山区一模)已知:如图,M是AB的中点,以AM为直径的⊙O与BP相切于点N,OP∥MN. 已知:如图,D是AB上一点,E是AC上的一点,BE、CD相交于点F,∠A=62°,∠ACD=35°,∠ABE=20°.求:(1)∠BDC的度数; (2)∠BFD的度数.
已知:如图,D是AB上一点,E是AC上的一点,BE、CD相交于点F,∠A=62°,∠ACD=35°,∠ABE=20°.求:(1)∠BDC的度数; (2)∠BFD的度数.