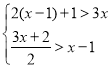题目内容
【题目】已知关于x的一元二次方程x2﹣2（a+1）x+a2+3＝0有两个实数根x1，x2
（1）求实数a的取值范围
（2）若等腰△ABC的三边长分别为x1，x2，6，求△ABC的周长
（3）是否存在实数a，使x1，x2恰是一个边长为
的菱形的两条对角线的长？若存在，求出这个菱形的面积；若不存在，说明理由．
【答案】（1）a≥1；（2）14；（3）存在，4．
【解析】
（1）根据一元二次方程根的判别式建立不等式求解即可；
（2）首先分x1＝x2，当x1＝6或x2＝6两种情况讨论，之后再分情况代入求出a的值再求出对应的x的值进一步计算即可；
（3）首先根据根与系数的关系得出x1+x2＝2（a+1），x1x2＝a2+3，根据勾股定理建立方程，然后进一步变形代入计算出a的值，然后利用菱形面积等于对角线乘积一半求出面积即可.
解：（1）根据题意得△＝4（a+1）2﹣4（a2+3）＝8a﹣8≥0， ∴a≥1；
（2）①当等腰△ABC底边为6，x1＝x2时，△＝0，则a＝1，
方程变形为x2﹣4x+4＝0，解得x1＝x2＝2，而2+2＜6，不符合三角形三边的关系，舍去；
②当等腰△ABC腰长为6，x1＝6或x2＝6时，把x＝6代入方程x2﹣2（a+1）x+a2+3＝0得36﹣12（a+1）+a2+3＝0，解得a1＝3，a2＝9，
当a＝3时，方程化为x2﹣8x+12＝0，解得x＝2或6，三角形三边为6、6、2，则△ABC的周长为6+6+2＝14；
当a＝9时，方程化为x2﹣20x+84＝0，解得x＝14或6，而6+6＜14，不符合三角形三边的关系，舍去；
∴△ABC的周长为14；
（3）存在．
由题意得：x1+x2＝2（a+1），x1x2＝a2+3，
∵
x12+
x22＝（
）2，
∴（x1+x2）2﹣2x1x2＝22，
即4（a+1）2﹣2（a2+3）＝88，
整理得a2+4a﹣45＝0，解得a1＝5，a2＝﹣9（舍去），
当a＝5，方程化为x2﹣12x+28＝0，则x1x2＝28，所以这个菱形的面积＝
×28＝14．
