Question

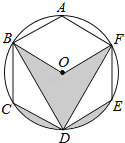
【题目】如图，正六边形ABCDEF内接于⊙O，若⊙O的半径为4，则阴影部分的面积等于 ．

Answer 1

【答案】π．

【解析】

试题分析：先正确作辅助线，构造扇形和等边三角形、直角三角形，分别求出两个弓形的面积和两个三角形面积，即可求出阴影部分的面积．

解：连接OC、OD、OE，OC交BD于M，OE交DF于N，过O作OZ⊥CD于Z，

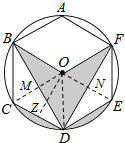
∵六边形ABCDEF是正六边形，

∴BC=CD=DE=EF，∠BOC=∠COD=∠DOE=∠EOF=60°，

由垂径定理得：OC⊥BD，OE⊥DF，BM=DM，FN=DN，

∵在Rt△BMO中，OB=4，∠BOM=60°，

∴BM=OB×sin60°=2，OM=OBcos60°=2，

∴BD=2BM=4，

∴△BDO的面积是×BD×OM=×4×2=4，

同理△FDO的面积是4；

∵∠COD=60°，OC=OD=4，

∴△COD是等边三角形，

∴∠OCD=∠ODC=60°，

在Rt△CZO中，OC=4，OZ=OC×sin60°=2，

∴S扇形OCD﹣S△COD=﹣×4×2=π﹣4，

∴阴影部分的面积是：4+4+π﹣4+π﹣4=π，

故答案为：π．