题目内容
【题目】在平面直角坐标系xOy中,抛物线y=﹣x2+2mx﹣m2+1的对称轴是直线x=1.
(1)求抛物线的表达式;
(2)点D(n,y1),E(3,y2)在抛物线上,若y1<y2,请直接写出n的取值范围;
(3)设点M(p,q)为抛物线上的一个动点,当﹣1<p<2时,点M关于y轴的对称点都在直线y=kx﹣4的上方,求k的取值范围.
【答案】(1)y=﹣x2+2x.(2)当n<﹣1或n>3时,y1<y2.(3)见解析
【解析】
试题分析:(1)由抛物线的对称轴方程可求得m=1,从而可求得抛物线的表达式;
(2)将x=3代入抛物线的解析式,可求得y2=3,将y=3代入抛物线的解析式可求得x1=﹣1,x2=3,由抛物线的开口向下,可知当当n<﹣1或n>3时,y1<y2;
(3)先根据题意画出点M关于y轴对称点M′的轨迹,然后根据点M关于y轴的对称点都在直线y=kx﹣4的上方,列出关于k的不等式组即可求得k的取值范围.
解:(1)∵抛物线的对称轴为x=1,
∴x=﹣![]() =﹣
=﹣![]() =1.
=1.
解得:m=1.
∴抛物线的解析式为y=﹣x2+2x.
(2)将x=3代入抛物线的解析式得y=﹣32+2×3=﹣3.
将y=﹣3代入得:﹣x2+2x=﹣3.
解得:x1=﹣1,x2=3.
∵a=﹣1<0,
∴当n<﹣1或n>3时,y1<y2.
(3)设点M关于y轴对称点为M′,则点M′运动的轨迹如图所示:
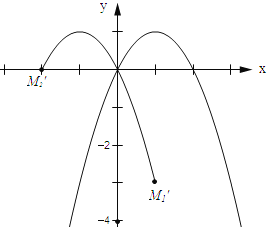
∵当P=﹣1时,q=﹣(﹣1)2+2×(﹣1)=﹣3.
∴点M关于y轴的对称点M1′的坐标为(1,﹣3).
∵当P=2时,q=﹣22+2×2=0,
∴点M关于y轴的对称点M2′的坐标为(﹣2,0).
①当k<0时,
∵点M关于y轴的对称点都在直线y=kx﹣4的上方,
∴﹣2k﹣4≤0.
解得:k≥﹣2.
②当k>0时,
∵点M关于y轴的对称点都在直线y=kx﹣4的上方,
∴k﹣4≤﹣3.
解得;k≤1.
∴k的取值范围是﹣2≤k≤1.