Question

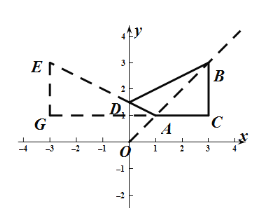
【题目】如图，在直角坐标系中，点，是第一象限角平分线上的两点，点的纵坐标为1，且，在轴上取一点，连接，，，，使得四边形的周长最小，这个最小周长的值为________．

Answer 1

【答案】

【解析】

先求出AC=BC=2，作点B关于y轴对称的点E，连接AE，交y轴于D，此时AE=AD+BD，且AD+BD值最小，即此时四边形的周长最小；作FG∥y轴，AG∥x轴，交于点G，则GF⊥AG，根据勾股定理求出AE即可．

解：∵，点的纵坐标为1，

∴AC∥x轴，

∵点，是第一象限角平分线上的两点，

∴∠BAC=45°，

∵，

∴∠BAC=∠ABC=45°，

∴∠C=90°，

∴BC∥y轴，

∴AC=BC=2，

作点B关于y轴对称的点E，连接AE，交y轴于D，此时AE=AD+BD，且AD+BD值最小，

∴此时四边形的周长最小，

作FG∥y轴，AG∥x轴，交于点G，则GF⊥AG，

∴EG=2，GA=4，

在Rt△AGE中，

，

∴ 四边形的周长最小值为2+2+=4+ ．