Question

【题目】如图，抛物线y=x2+bx+c与x轴交于A、B两点，B点坐标为（3，0），与y轴交于点C（0，﹣3）
（1）求抛物线的解析式；
（2）点P在抛物线位于第四象限的部分上运动，当四边形ABPC的面积最大时，求点P的坐标和四边形ABPC的最大面积．
（3）直线l经过A、C两点，点Q在抛物线位于y轴左侧的部分上运动，直线m经过点B和点Q，是否存在直线m，使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似？若存在，求出直线m的解析式，若不存在，请说明理由．

Answer 1

【答案】
（1）

解：把B、C两点坐标代入抛物线解析式可得 ，解得 ，

∴抛物线解析式为y=x2﹣2x﹣3

（2）

解：如图1，连接BC，过Py轴的平行线，交BC于点M，交x轴于点H，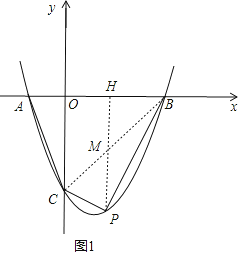

在y=x2﹣2x﹣3中，令y=0可得0=x2﹣2x﹣3，解得x=﹣1或x=3，

∴A点坐标为（﹣1，0），

∴AB=3﹣（﹣1）=4，且OC=3，

∴S△ABC= ABOC= ×4×3=6，

∵B（3，0），C（0，﹣3），

∴直线BC解析式为y=x﹣3，

设P点坐标为（x，x2﹣2x﹣3），则M点坐标为（x，x﹣3），

∵P点在第四限，

∴PM=x﹣3﹣（x2﹣2x﹣3）=﹣x2+3x，

∴S△PBC= PMOH+ PMHB= PM（OH+HB）= PMOB= PM，

∴当PM有最大值时，△PBC的面积最大，则四边形ABPC的面积最大，

∵PM=﹣x2+3x=﹣（x﹣ ）2+ ，

∴当x= 时，PMmax= ，则S△PBC= × = ，

此时P点坐标为（ ，﹣ ），S四边形ABPC=S△ABC+S△PBC=6+ = ，

即当P点坐标为（ ，﹣ ）时，四边形ABP的面积最大，最大面积为 ；

（3）

解：如图2，设直线m交y轴于点N，交直线l于点G，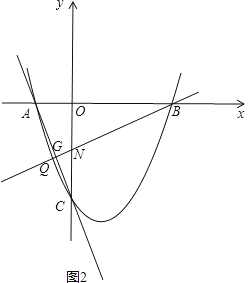

则∠AGP=∠GNC+∠GCN，

当△AGB和△NGC相似时，必有∠AGB=∠CGB，

又∠AGB+∠CGB=180°，

∴∠AGB=∠CGB=90°，

∴∠ACO=∠OBN，

在Rt△AON和Rt△NOB中

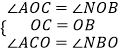
∴Rt△AON≌Rt△NOB（ASA），

∴ON=OA=1，

∴N点坐标为（0，﹣1），

设直线m解析式为y=kx+d，把B、N两点坐标代入可得 ，解得 ，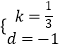

∴直线m解析式为y= x﹣1，

即存在满足条件的直线m，其解析式为y= x﹣1

【解析】（1）由B、C两点的坐标，利用待定系数法可求得抛物线的解析式；
（2）连接BC，则△ABC的面积是不变的，过P作PM∥y轴，交BC于点M，设出P点坐标，可表示出PM的长，可知当PM取最大值时△PBC的面积最大，利用二次函数的性质可求得P点的坐标及四边形ABPC的最大面积；
（3）设直线m与y轴交于点N，交直线l于点G，由于∠AGP=∠GNC+∠GCN，所以当△AGB和△NGC相似时，必有∠AGB=∠CGB=90°，则可证得△AOC≌△NOB，可求得ON的长，可求出N点坐标，利用B、N两的点坐标可求得直线m的解析式．本题为二次函数的综合应用，涉及知识点有待定系数法、二次函数的最值、相似三角形的判定、全等三角形的判定和性质等．在（2）中确定出PM的值最时四边形ABPC的面积最大是解题的关键，在（3）中确定出满足条件的直线m的位置是解题的关键．本题考查知识点较多，综合性较强，特别是第（2）问和第（3）问难度较大．
【考点精析】根据题目的已知条件，利用抛物线与坐标轴的交点和相似三角形的判定的相关知识可以得到问题的答案，需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标．因此一元二次方程中的b2-4ac，在二次函数中表示图像与x轴是否有交点．当b2-4ac>0时，图像与x轴有两个交点；当b2-4ac=0时，图像与x轴有一个交点；当b2-4ac<0时，图像与x轴没有交点．；相似三角形的判定方法:两角对应相等，两三角形相似（ASA）；直角三角形被斜边上的高分成的两个直角三角形和原三角形相似； 两边对应成比例且夹角相等，两三角形相似（SAS）；三边对应成比例，两三角形相似（SSS）．