题目内容
【题目】如图，已知抛物线y=﹣
x2﹣
x+2与x轴交于A、B两点，与y轴交于点C.
⑴求点A，B，C的坐标；
⑵点E是此抛物线上的点，点F是其对称轴上的点，求以A，B，E，F为顶点的平行四边形的面积；
⑶此抛物线的对称轴上是否存在点M，使得△ACM是等腰三角形？若存在，请求出点M的坐标；若不存在，请说明理由．
【答案】（1）（0，2）（2）
（3）（﹣1，﹣1）或（﹣1，2+
）或（﹣1，2﹣
）．
【解析】（1）分别令y=0，x=0，即可解决问题；（2）由图象可知AB只能为平行四边形的边，易知点E坐标（﹣7，﹣ 
）或（5，﹣
），由此不难解决问题；（3）分A、C、M为顶点三种情形讨论，分别求解即可解决问题．
解：（1）令y=0得﹣
x2﹣
x+2=0，∴x2+2x﹣8=0，
x=﹣4或2，∴点A坐标（2，0），点B坐标（﹣4，0），
令x=0，得y=2，∴点C坐标（0，2）．
（2）由图象可知AB只能为平行四边形的边，
∵AB=EF=6，对称轴x=﹣1，
∴点E的横坐标为﹣7或5，∴点E坐标（﹣7，﹣ 
）或（5，﹣
），此时点F（﹣1，﹣
）
∴以A，B，E，F为顶点的平行四边形的面积=6×
=
．
（3）如图所示，
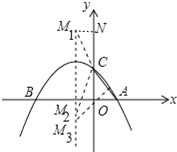
①当C为顶点时，CM1=CA，CM2=CA，作M1N⊥OC于N，
在RT△CM1N中，CN=
=
，
∴点M1坐标（﹣1，2+
），点M2坐标（﹣1，2﹣
）．
②当M3为顶点时，
∵直线AC解析式为y=﹣x+2，线段AC的垂直平分线为y=x，
∴点M3坐标为（﹣1，﹣1）．
③当点A为顶点的等腰三角形不存在．
综上所述点M坐标为（﹣1，﹣1）或（﹣1，2+
）或（﹣1，2﹣
）．
“点睛”本题考查二次函数综合题、平行四边形的判定和性质、勾股定理等知识，解题的关键是熟练掌握抛物线与坐标轴交点的求法，学会分类讨论的思想，属于中考压轴题．
