题目内容
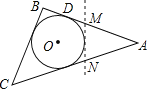
【题目】如图,△ABC是一张周长为22cm的三角形纸片,BC=6cm,⊙O是它的内切圆,小明准备用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN,则剪下的三角形的周长为_____.
【答案】10cm.
【解析】
根据圆的切线长定理可知BD=BE,CE=CF,MD=MG,NG=NF,即可求出剪下的三角形AMN的周长.
解:△ABC的内切圆与三边分别相切于D、E、F,MN与⊙O相切于G,如图,
则BD=BE,CE=CF,MD=MG,NG=NF,
∵BC=6,即CE+BE=6,
∴BD+BE+CE+CF=12,
∴剪下的三角形AMN的周长=AM+MG+NG+AN=AM+MD+NF+AN=AD+AF=22cm﹣12cm=10(cm).
故答案为:10cm.

练习册系列答案
相关题目
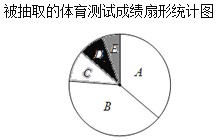
【题目】有一学校为了解九年级学生某次的体育测试成绩,现对这次体育测试成绩进行随机抽样调查,结果统计如下,其中扇形统计图中C等级所在扇形的圆心角为36°.
被抽取的体育测试成绩频数分布表
等级 | 成绩(分) | 频数(人数) |
A | 36<x≤40 | 19 |
B | 32<x≤36 | b |
C | 28<x≤32 | 5 |
D | 24<x≤28 | 4 |
E | 20<x≤24 | 2 |
合计 | a | |
请你根据以上图表提供的信息,解答下列问题:
(1)a= ,b= ;
(2)A等级的频率是 ;
(3)在扇形统计图中,B等级所对应的圆心角是 度;
(4)已知该校九年级共有780学生,估计成绩(分)在32<x≤36之间的学生约有 人.