题目内容
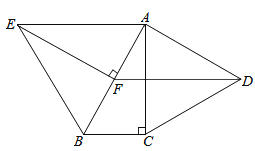
【题目】如图，△ABC的周长为26，点D，E都在边BC上，∠ABC的平分线垂直于AE，垂足为Q，∠ACB的平分线垂直于AD，垂足为P，若BC=10，则PQ的长为（ ）
A.
B.
C.3
D.4
【答案】C
【解析】∵BQ平分∠ABC，BQ⊥AE，∴△BAE是等腰三角形。
同理△CAD是等腰三角形。
∴点Q是AE中点，点P是AD中点（三线合一）。∴PQ是△ADE的中位线。
∵BE+CD=AB+AC=26﹣BC=26﹣10=16，∴DE=BE+CD﹣BC=6。
∴PQ=
DE=3.故选C.
【考点精析】解答此题的关键在于理解三角形中位线定理的相关知识，掌握连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
