题目内容
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.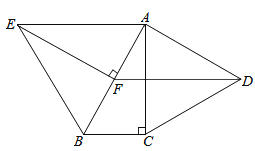
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
【答案】
(1)
【解答】证明:∵Rt△ABC中,∠BAC=30°,
∴AB=2BC,
又∵△ABE是等边三角形,EF⊥AB,
∴AB=2AF
∴AF=BC,
在Rt△AFE和Rt△BCA中
![]()
∴△AFE≌△BCA(HL),
∴AC=EF;
(2)
【解答】∵△ACD是等边三角形,
∴∠DAC=60°,AC=AD,
∴∠DAB=∠DAC+∠BAC=90°
又∵EF⊥AB,
∴EF∥AD,
∵AC=EF,AC=AD,
∴EF=AD,
∴四边形ADFE是平行四边形.
【解析】(1)首先Rt△ABC中,由∠BAC=30°可以得到AB=2BC,又因为△ABE是等边三角形,EF⊥AB,由此得到AE=2AF,并且AB=2AF,然后即可证明△AFE≌△BCA,再根据全等三角形的性质即可证明AC=EF;(2)根据(1)知道EF=AC,而△ACD是等边三角形,所以EF=AC=AD,并且AD⊥AB,而EF⊥AB,由此得到EF∥AD,再根据平行四边形的判定定理即可证明四边形ADFE是平行四边形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


