题目内容
【题目】如图,⊙O的半径r=25,四边形ABCD内接圆⊙O,AC⊥BD于点H,P为CA延长线上的一点,且∠PDA=∠ABD
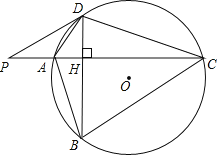
(1) 试判断PD与⊙O的位置关系,并说明理由
(2) 若tan∠ADB=![]() ,PA=
,PA=![]() AH,求BD的长
AH,求BD的长
【答案】(1)PD与圆O相切.理由见解析;(2)25![]()
【解析】
试题分析:(1)首先连接DO并延长交圆于点E,连接AE,由DE是直径,可得∠DAE的度数,又由∠PDA=∠ABD=∠E,可证得PD⊥DO,即可得PD与圆O相切于点D;
(2)首先由tan∠ADB=![]() ,可设AH=3k,则DH=4k,又由PA=
,可设AH=3k,则DH=4k,又由PA=![]() AH,易求得∠P=30°,∠PDH=60°,连接BE,则∠DBE=90°,DE=2r=50,可得BD=DE
AH,易求得∠P=30°,∠PDH=60°,连接BE,则∠DBE=90°,DE=2r=50,可得BD=DE![]() cos30°=25
cos30°=25![]()
试题解析:(1)PD与圆O相切.
理由:如图,连接DO并延长交圆于点E,连接AE,

∵DE是直径,
∴∠DAE=90°,
∴∠AED+∠ADE=90°,
∵∠PDA=∠ABD=∠AED,
∴∠PDA+∠ADE=90°,
即PD⊥DO,
∴PD与圆O相切于点D;
(2)∵tan∠ADB=![]()
∴可设AH=3k,则DH=4k,
∵PA=![]() AH,
AH,
∴PA=(4![]() -3)k,
-3)k,
∴PH=4![]() k,
k,
∴在Rt△PDH中,tan∠P=![]() ,
,
∴∠P=30°,∠PDH=60°,
∵PD⊥DO,
∴∠BDE=90°-∠PDH=30°,
连接BE,则∠DBE=90°,DE=2r=50,
∴BD=DE![]() cos30°=25
cos30°=25![]()

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目