题目内容
【题目】如图,抛物线y=﹣![]() x2+mx+2与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴直线x=
x2+mx+2与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴直线x=![]() 交x轴于点D.
交x轴于点D.

(1)求m的值;
(2)在抛物线的对称轴上找出点P,使△PCD是以CD为腰的等腰三角形,直接写出P点的坐标;
(3)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,与x轴相交于点H,连接CF、BF、OE,当四边形CDBF的面积最大时,请你说明四边形OCFE的形状.
【答案】(1)![]() (2)P1(
(2)P1(![]() ,
,![]() ),P2(
),P2(![]() ,﹣
,﹣![]() ),P3(
),P3(![]() ,4)(3)平行四边形
,4)(3)平行四边形
【解析】
试题分析:(1)根据对称轴公式,可得m的值;
(2)根据等腰三角形的定义,可得P点坐标;
(3)根据平行于y轴的直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得EF的长,根据三角形的面积公式,可得二次函数,根据二次函数的性质,可得n的值,根据平行四边形的判定,可得答案.
试题解析:(1)∵对称轴是直线x=![]() ,
,
∴﹣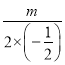 =
=![]() ,
,
∴m=![]() ;
;
(2)由勾股定理,得
CD=![]() ,当CD=DP=
,当CD=DP=![]() 时,P(
时,P(![]() ,
,![]() ),(
),(![]() ,﹣
,﹣![]() ),
),
当CD=CP时,设P点坐标为(![]() ,b),
,b),
∴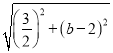 =
=![]() ,
,
解得b=4,P(![]() ,4),
,4),
综上所述:P1(![]() ,
,![]() ),P2(
),P2(![]() ,﹣
,﹣![]() ),P3(
),P3(![]() ,4);
,4);
(3)四边形OCFE是平行四边形,
由抛物线y=﹣![]() x2+
x2+![]() x+2,
x+2,
令y=0,﹣![]() x2+
x2+![]() x+2=0,解得x1=﹣1,x2=4,
x+2=0,解得x1=﹣1,x2=4,
∴B(4,0),A(﹣1,0),
当x=0时,y=2,即C(0,2),
设BC的解析式为y=kx+b,把B(4,0),C(0,2)代入,得
![]() ,解得
,解得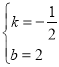 ,
,
直线BC解析式为y=﹣![]() x+2.
x+2.
点F在抛物线上,设F的坐标为(n,﹣![]() n2+
n2+![]() n+2),
n+2),
点E在BC上,E点的坐标为(n,﹣![]() n+2),
n+2),
EF=FH﹣EH=﹣![]() n2+2n,
n2+2n,
∵![]() ,
,
![]() =
=![]() BD·CO=
BD·CO=![]() ×(4﹣1.5)×2=
×(4﹣1.5)×2=![]() ,
,![]() =
=![]() EF·OB=
EF·OB=![]() ×4×(﹣
×4×(﹣![]() n2+2n)=﹣n2+4n,
n2+2n)=﹣n2+4n,
![]() =﹣n2+4n+
=﹣n2+4n+![]() =﹣(n﹣2)2+
=﹣(n﹣2)2+![]() ,
,
当n=2时,四边形CDBF的面积最大,此时EF=﹣![]() n2+2n=2,EH=﹣
n2+2n=2,EH=﹣![]() n+2=1,OH=2,OE=
n+2=1,OH=2,OE=![]() =
=![]() .
.
∵OC=EF=2,OC∥EF,
∴四边形OCFE是平行四边形.